 I am a regular reader of Ash Jogalekar’s blog Curious Wavefunction, but I found my way to his latest via the eclectic website 3 Quarks Daily, also highly recommended. I could not resist the title, “Mathematics, And The Excellence Of The Life It Brings”. The entirety of the post was about the mathematician Shing-Tung Yau’s recent memoir, The Shape of a Life, but Jogalekar’s introductory remarks about his personal involvement with mathematics stirred so many personal recollections of my own, that I thought I would provide an excerpt, followed by my own comments. Furthermore, he also addresses in passing the perennial question of whether math is invented or discovered.
I am a regular reader of Ash Jogalekar’s blog Curious Wavefunction, but I found my way to his latest via the eclectic website 3 Quarks Daily, also highly recommended. I could not resist the title, “Mathematics, And The Excellence Of The Life It Brings”. The entirety of the post was about the mathematician Shing-Tung Yau’s recent memoir, The Shape of a Life, but Jogalekar’s introductory remarks about his personal involvement with mathematics stirred so many personal recollections of my own, that I thought I would provide an excerpt, followed by my own comments. Furthermore, he also addresses in passing the perennial question of whether math is invented or discovered.
See Math and the Excellence of Life
(Update 8/9/2021) Jogalekar’s story about his embracing math and the effect Simmon’s topology book had on him is even more amazing than I thought. Throughout his younger years he had always been labeled “bad at math” and did poorly in school. But a teacher and Simmon’s book changed all that. He explains in a recent article in 3QuarksDaily, which I also provide here.
I can’t help singling out a section where he, too, extols the significance and importance of high school geometry (see my post “Down with Geometry”):
“… Purely through accident at this time, I had gotten my hands on a book on topology, a subject that I had become mildly interested in because of its deep connections to geometry; interestingly, while I was rather abysmal at algebra in school, I always did well with geometry because I was good at visualization. …
The topology book and the professor completely changed my outlook and saved me. I started doing well and tackling advanced topics and started to love math. I also got interested in physics and did well. Most importantly, I started appreciating the beauty of math. Over time I found that people interested in mathematics are generally of two kinds, although there’s some overlap: there are those who really enjoy mathematical puzzles and puzzle-like problems, relishing the raw process of problem-solving. Then there are others who simply enjoy the abstract nature of proofs and the connections between different topics: I am definitely part of this second group. In fact, another revelation I had was that most of the high school curriculum needed the students to be good at the former skill and had no appreciation of the latter, thus simply weeding out students like myself who wanted to understand the big picture and see the connections rather than just become adept at problem-solving.”
I confess I share this view and find it somewhat ironic that my website has devolved into a problem-solving source. I have tried to show the wider picture of fascinating connections, but that often takes more skill and time than I currently possess.
![]() This problem from Colin Hughes at Maths Challenge is a most surprising result that takes a bit of tinkering to solve.
This problem from Colin Hughes at Maths Challenge is a most surprising result that takes a bit of tinkering to solve.
 I am a regular reader of Ash Jogalekar’s blog
I am a regular reader of Ash Jogalekar’s blog  This 2007 four-star problem from Colin Hughes at Maths Challenge is definitely a bit challenging.
This 2007 four-star problem from Colin Hughes at Maths Challenge is definitely a bit challenging. This is another intriguing problem from Presh Talwalkar.
This is another intriguing problem from Presh Talwalkar. This interesting problem comes from Colin Hughes at the Maths Challenge website.
This interesting problem comes from Colin Hughes at the Maths Challenge website. A glutton for punishment I considered another Sam Loyd puzzle:
A glutton for punishment I considered another Sam Loyd puzzle: This is from the UKMT Senior Challenge of 2004.
This is from the UKMT Senior Challenge of 2004.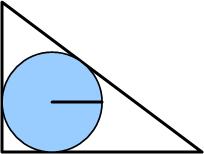 This statement showed up recently at
This statement showed up recently at 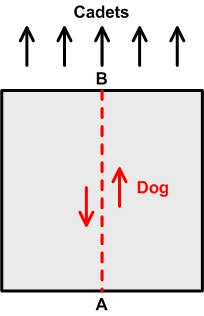 In my search for new problems I came across this one from Martin Gardner:
In my search for new problems I came across this one from Martin Gardner: This is a delightful little problem from Dick Hess that exercises one’s basic facility with logarithms:
This is a delightful little problem from Dick Hess that exercises one’s basic facility with logarithms: