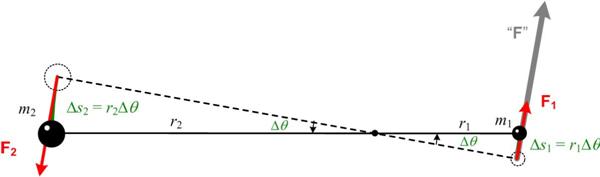
I have always had a tenuous relationship with the concept of angular momentum, but recently my concerns resurfaced when I did my studies on Kepler, and in particular his “equal areas law” and Newton’s elegant geometric proof. I love the fact that a simple geometric argument, seemingly totally divorced from the physical situation, can provide an explanation for why the line from the Sun to a planet sweeps out equal areas in equal time as the planet orbits the Sun, solely under the influence of the gravitational force between them. However, modern physics books invariably cite the conservation of angular momentum as the “explanation.” I indicated before in my “Kepler’s Laws and Newton’s Laws” essay that this “explanation” irritated me. In this essay I go into detail about my reservations concerning this line of argument. See Angular Momentum.
Tag Archives: angular momentum
Kepler’s Equal Areas Law
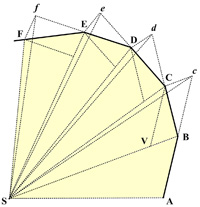I have long been fascinated by Newton’s proof of Kepler’s Equal Areas Law and wanted to write about it. Of course, others have as well, but I wanted to emphasize an aspect of the proof that supported my philosophy of mathematics.
Before I get to Newton, however, I wanted to discuss how Kepler himself justified this law, since his approach has a number of fascinating historical aspects to it. I have previously discussed Kepler’s ellipse and in the process of doing that research, I came across a number of articles about how Kepler arrived at his equal areas law. One notable result is that even though now we call the idea that a planet orbits the Sun in an elliptical path with the Sun at one focus, Kepler’s First Law, and the idea that the line from the Sun to the planet sweeps out equal areas in equal times, Kepler’s Second Law, Kepler actually discovered these laws in reverse order. See Kepler’s Equal Areas Law