 Since the changes in Twitter (now X), I have not been able to see the posts, not being a subscriber. But I noticed poking around that some twitter accounts were still viewable. However, like some demented aging octogenarian they had lost track of time, that is, instead of being sorted with the most recent post first, they showed a random scattering of posts from different times. So a current post could be right next to one several years ago. That is what I discovered with the now defunct MathsMonday site. I found a post from 10 May 2021 that I had not seen before, namely,
Since the changes in Twitter (now X), I have not been able to see the posts, not being a subscriber. But I noticed poking around that some twitter accounts were still viewable. However, like some demented aging octogenarian they had lost track of time, that is, instead of being sorted with the most recent post first, they showed a random scattering of posts from different times. So a current post could be right next to one several years ago. That is what I discovered with the now defunct MathsMonday site. I found a post from 10 May 2021 that I had not seen before, namely,
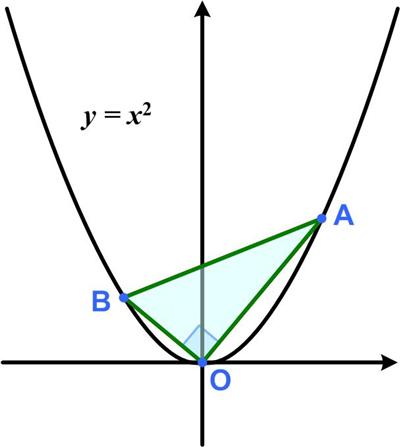
“The points A and B are on the curve y = x2 such that AOB is a right angle. What points A and B will give the smallest possible area for the triangle AOB?”
See the Pythagorean Parabola Puzzle for solution.
(Update 9/1/2023) Elegant Alternative Solution by Oscar Rojas
Continue reading

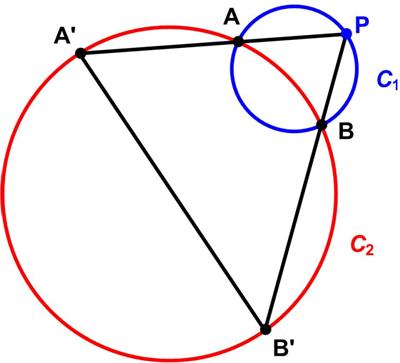 This is a Maths Item of the Month (MIOM)
This is a Maths Item of the Month (MIOM)  This is a belated Christmas puzzle from December 2019
This is a belated Christmas puzzle from December 2019 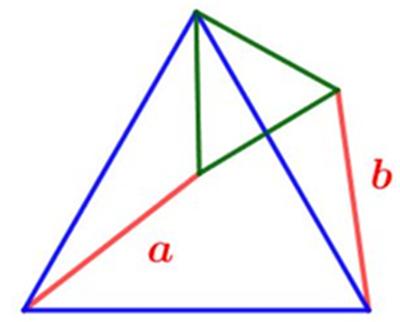 This is another problem from MEI’s MathsMonday.
This is another problem from MEI’s MathsMonday.
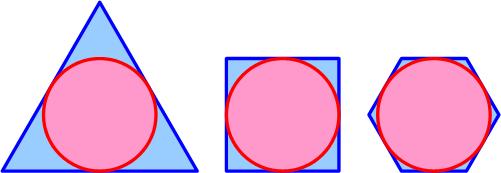 This surprising, but simple, puzzle is from the 12 April MathsMonday
This surprising, but simple, puzzle is from the 12 April MathsMonday 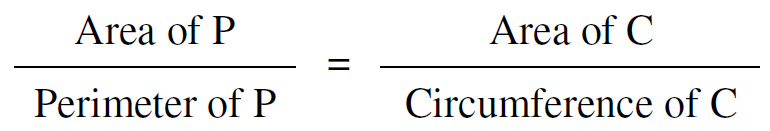
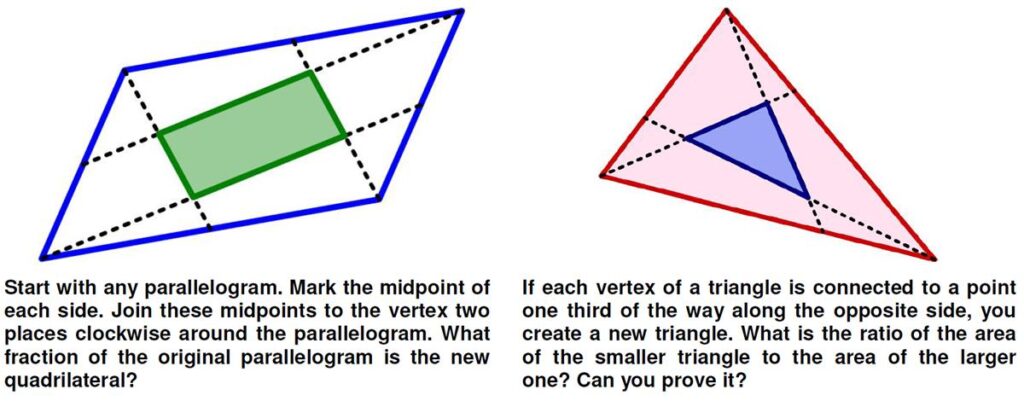 These two interesting problems were posed on MEI’s MathsMonday site on
These two interesting problems were posed on MEI’s MathsMonday site on 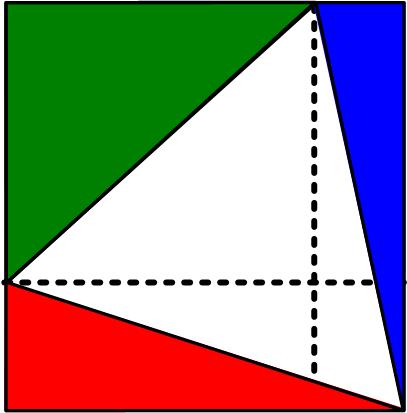 This simple-appearing problem is from the 17 August 2020 MathsMonday
This simple-appearing problem is from the 17 August 2020 MathsMonday