 In my search for problems I decided to purchase Dan Griller’s GCSE problem book mentioned in the Cube Roots Problem. I am still a bit confused about the purpose of the GCSE exam and who it is for, since the other problems in Griller’s book are often as challenging or more so than the cube roots problem. It is hard to believe students not pursuing college level degrees could solve these problems. (Grades 8 and 9 referred to in the subtitle of the book must indicate something other than US grades 8 and 9, since the exams are aimed at 16 year-olds, not 13 and 14 year-olds.)
In my search for problems I decided to purchase Dan Griller’s GCSE problem book mentioned in the Cube Roots Problem. I am still a bit confused about the purpose of the GCSE exam and who it is for, since the other problems in Griller’s book are often as challenging or more so than the cube roots problem. It is hard to believe students not pursuing college level degrees could solve these problems. (Grades 8 and 9 referred to in the subtitle of the book must indicate something other than US grades 8 and 9, since the exams are aimed at 16 year-olds, not 13 and 14 year-olds.)
Supposedly the problems in Griller’s book are nominally arranged in increasing order of difficulty from problem 1 to problem 75. However it seemed to me that there were challenging problems scattered throughout and the last problem was not all that much harder than earlier ones. And many of them had a whiff of Coffin Problems—they seemed impossible at first (Problem 44: Construct a 67.5° angle!). I don’t know how many problems are on the exam or how long the exam is, but anyone taking a timed exam does not have the leisure to mull over a problem. The student only has a few minutes to come up with an approach and clever insights are rare under the circumstances. Anyway, here is the last problem in the book.
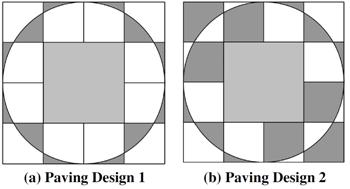
“Problem 75. A square pond of side length 2 metres is to be surrounded by twelve square paving stones of side length 1 metre.
(a) The first design is constructed with a circle whose centre coincides with the centre of the pond. Calculate exactly the total dark grey area for this design.
(b) The second design is similar. Calculate exactly the total dark grey area for this second design.”
Answer.
See the Pool Paving Problem for solutions.
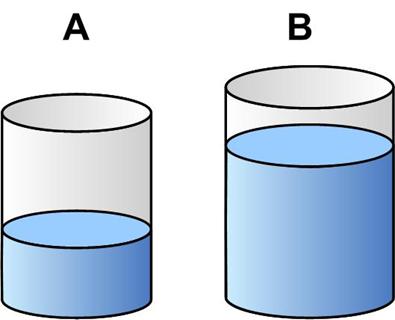 This is a slightly different type of a mixture problem from Dan Griller.
This is a slightly different type of a mixture problem from Dan Griller.
 This is a slightly challenging problem from Dan Griller.
This is a slightly challenging problem from Dan Griller. This is a classic example of a mixture problem from Dan Griller that recalls my agonies of beginning algebra.
This is a classic example of a mixture problem from Dan Griller that recalls my agonies of beginning algebra. In my search for problems I decided to purchase Dan Griller’s GCSE problem book mentioned in the
In my search for problems I decided to purchase Dan Griller’s GCSE problem book mentioned in the  In a June Chalkdust
In a June Chalkdust