 Here is another problem from the 2020 Math Calendar.
Here is another problem from the 2020 Math Calendar.
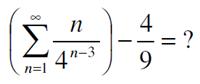
As a hint, recall that all the answers are integer days of the month. And the solution employs a technique familiar to these pages.
See Autumn Sum for a solution.

 Here is another problem from the 2020 Math Calendar.
Here is another problem from the 2020 Math Calendar.
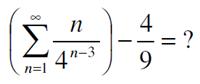
As a hint, recall that all the answers are integer days of the month. And the solution employs a technique familiar to these pages.
See Autumn Sum for a solution.
 Here is another problem from the 2020 Math Calendar to stimulate your mind.
Here is another problem from the 2020 Math Calendar to stimulate your mind.![]()
Remember that the answers to Math Calendar problems must all be whole numbers representing days of the month.
See New Years Sum for a solution.
![]() This is a stimulating little problem from the ever-creative James Tanton:
This is a stimulating little problem from the ever-creative James Tanton:
“An ant is at the east end of an infinite stretchy band, initially 2 ft long. Each day: ant walks 1 ft west on the band. Overnight while sleeping, band stretches to double its length (carrying ant westward as does so). Same routine each day/night. Will ant cover 99% of band’s length?”
(Ant from clipart-library.com)
See the Rubber Band Ant for solutions.
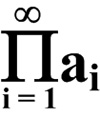 This is a challenging problem from Mathematical Quickies (1967).
This is a challenging problem from Mathematical Quickies (1967).
“Evaluate the infinite product:![]() ”
”
I came up with a motivated solution using some standard techniques from calculus. Mathematical Quickies had a solution that did not employ calculus, but one which I felt used unmotivated tricks.
See the Infinite Product Problem for solutions.
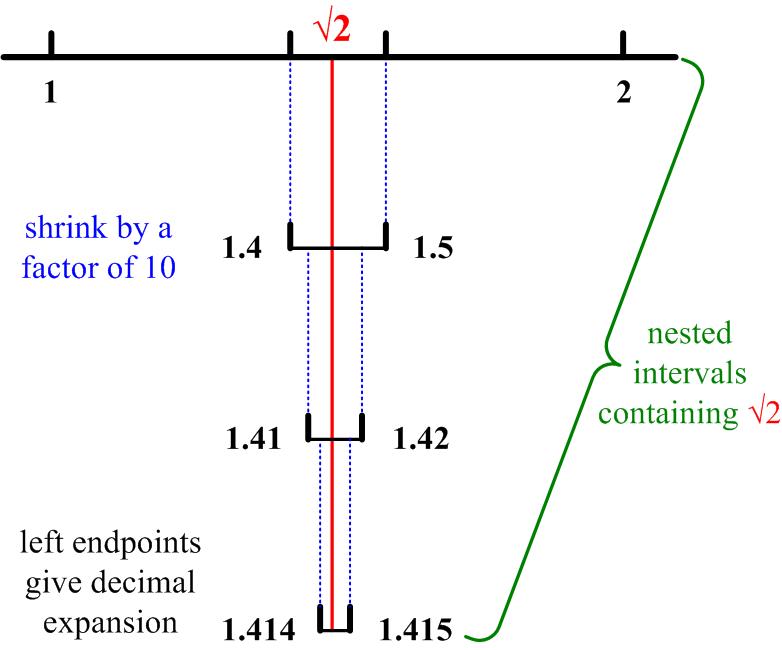 Probably the most satisfying article I have put together is a recent one on point set topology. An old friend of mine, who studied math and physics in college but ended up getting a doctorate in English, asked me, what was topology? Knowing that there were two main branches of topology (general or point set topology and algebraic topology), I chose to describe point set topology first, especially since it was what I was most familiar with and had worked with most in my graduate work.
Probably the most satisfying article I have put together is a recent one on point set topology. An old friend of mine, who studied math and physics in college but ended up getting a doctorate in English, asked me, what was topology? Knowing that there were two main branches of topology (general or point set topology and algebraic topology), I chose to describe point set topology first, especially since it was what I was most familiar with and had worked with most in my graduate work.
The essay turned out to have a surprising structure more like a musical theme and variations. The theme was the geometric series. I found it to be a wonderful medium to show the evolution of ideas (acting as variations) from the early Greeks (Zeno’s Paradoxes) through the development of calculus, decimal expansions of real numbers, to power series, metric spaces, and finally general topologies.
There was an additional benefit to this series of transformations of an initial idea: one of the major aspects of true mathematics became evident, namely, the extension of an idea into new territories that reveal unexpected connections to other forms of mathematics. Treating complicated functions as points in a topological space was a wonderful idea developed over the end of the 19th and beginning of the 20th centuries and became the basis of the field of functional analysis. See Point Set Topology (revised).
(Update 6/3/2021) Slightly revised version.
I happened to review this article and noticed I made a mistake in my integration example. I have no idea what I was thinking at the time, so I corrected it. As I reviewed the rest of the article, I noticed a bunch of “typos” that would make the text confusing, so I corrected those as well. And finally I rephrased wording in a couple of places to try to make things clearer.