 This is another nice problem from the 2025 Math Calendar.
This is another nice problem from the 2025 Math Calendar.
“The two squares in the diagram have areas 9 and 16 and form two of the sides of a triangle with area 3. What is the area x of the blue triangle?”
Again, the result must be a number of a day in a month.
See the Two Squares Puzzle for a solution.

 This is another challenging sum from the 2024 Math Calendar.
This is another challenging sum from the 2024 Math Calendar.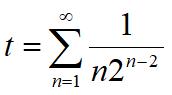 ”
”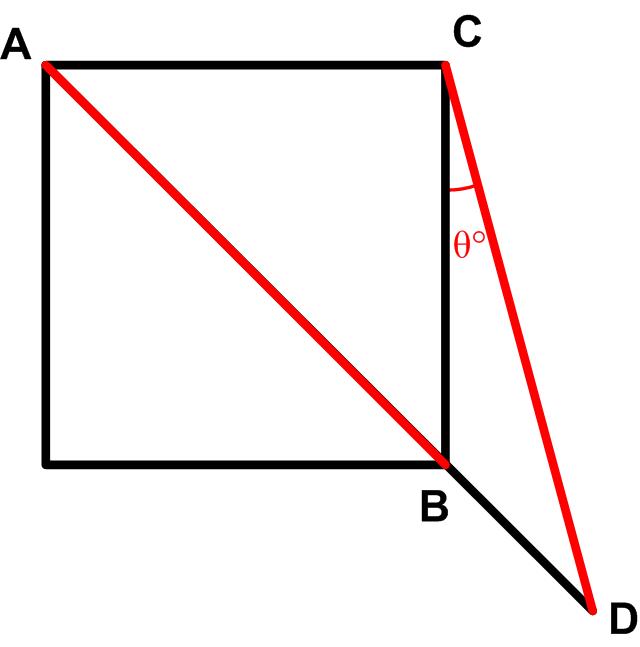 For me this turned out to be sort of a challenging problem from the 2025 Math Calendar.
For me this turned out to be sort of a challenging problem from the 2025 Math Calendar. This is another simple problem from the 2025 Math Calendar.
This is another simple problem from the 2025 Math Calendar. This is a nice little puzzle from the 2024 Math Calendar.
This is a nice little puzzle from the 2024 Math Calendar. Well, I discovered that the 2024 Math Calendar has some interesting problems, so I guess things will limp along for a while. This is a challenging but imaginative problem from the calendar.
Well, I discovered that the 2024 Math Calendar has some interesting problems, so I guess things will limp along for a while. This is a challenging but imaginative problem from the calendar.
 This is another stimulating little problem from the 2022 Math Calendar.
This is another stimulating little problem from the 2022 Math Calendar.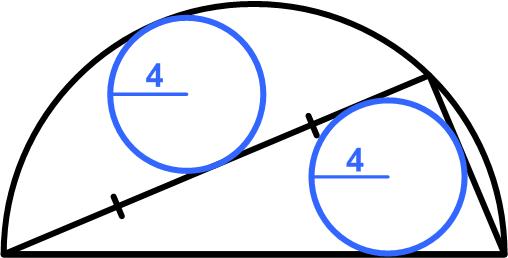 Here is a problem from the 2022 Math Calendar.
Here is a problem from the 2022 Math Calendar. Here is a tricky little logarithm problem from the 2021 Math Calendar.
Here is a tricky little logarithm problem from the 2021 Math Calendar. Here is another sum problem, this time from the 2021 Math Calendar.
Here is another sum problem, this time from the 2021 Math Calendar.