 The “Moving Up” post recalled an unforgettable moment in my past, when I still rode the Washington Metro somewhat sporadically (my youth was spent riding busses, before the advent of the Metro). It was the first time I confronted the escalator at the DuPont Circle stop. I was going to a math talk with a friend and we were busy discussing math when I stepped onto the escalator. Suddenly, I looked up and saw the stairs disappearing 188 feet into the heavens and froze. I have always been afraid of heights, and the escalator brought out all the customary terror. There was of course no turning back. And then people started bolting up the stairs past me, not always avoiding brushing by.
The “Moving Up” post recalled an unforgettable moment in my past, when I still rode the Washington Metro somewhat sporadically (my youth was spent riding busses, before the advent of the Metro). It was the first time I confronted the escalator at the DuPont Circle stop. I was going to a math talk with a friend and we were busy discussing math when I stepped onto the escalator. Suddenly, I looked up and saw the stairs disappearing 188 feet into the heavens and froze. I have always been afraid of heights, and the escalator brought out all the customary terror. There was of course no turning back. And then people started bolting up the stairs past me, not always avoiding brushing by.
My hand was clamped to the handrail in a death grip. I had to hold on even tighter as the sweat of fear made my hands slippery. In such situations I often feel a sense of vertigo or loss of balance. It was then that I thought the handrail was moving faster than the steps so that I was being pulled forward. I couldn’t tell if it was the vertigo or an actual movement. In any case, I periodically let go and repositioned my death grip. After an eternity, it was over, and I staggered out into the street. Needless to say, on our return I sought out the elevator. Fortunately, it was working—not always the case in the Washington Metro.
Once my brain was functioning a bit, I pondered the question of the relative speeds of the handrail and steps. How could they be synchronized? But after a while I left it as an interesting curiosity.
See Escalator Terror
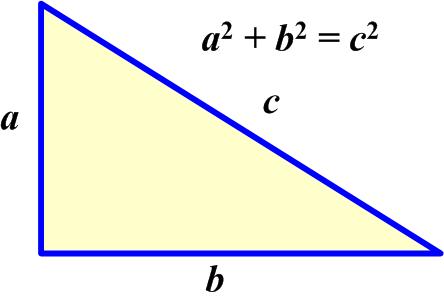 One of the joys of getting old is that you forget things. So one of the things I recall is that the converse of the Pythagorean Theorem is true, that is, if a triangle with short sides a and b and long side c is such that
One of the joys of getting old is that you forget things. So one of the things I recall is that the converse of the Pythagorean Theorem is true, that is, if a triangle with short sides a and b and long side c is such that
 One is reduced to hysterical laughter to try to maintain a modicum of sanity.
One is reduced to hysterical laughter to try to maintain a modicum of sanity.
 My cousin sent me this
My cousin sent me this  The “
The “ I thought it might be interesting to explore the mathematics of a common problem with a store-bought HO model train set that contains a collection of straight track segments and fixed-radius curved track segments that form a simple oval. Invariably an initial run of the train has it careening off the track when the train first meets the curved segment after running along the straight track segments.
I thought it might be interesting to explore the mathematics of a common problem with a store-bought HO model train set that contains a collection of straight track segments and fixed-radius curved track segments that form a simple oval. Invariably an initial run of the train has it careening off the track when the train first meets the curved segment after running along the straight track segments.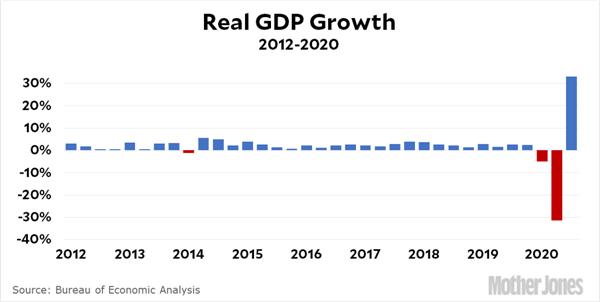 Twitter comments to the recently released GDP growth numbers for the Third Quarter reminded me of an old trap regarding percentages. The financial and technical articles were accurate, but the comments by Twitter users often reflected the pitfall.
Twitter comments to the recently released GDP growth numbers for the Third Quarter reminded me of an old trap regarding percentages. The financial and technical articles were accurate, but the comments by Twitter users often reflected the pitfall. Being born on February 29 I have always had an interest in the calendar and the mechanics of Leap Year. Since I am sure everyone knows about Leap Year, I will just rattle off a few trivia questions to stimulate the memory. Why was I excited about my birthday in 2000 when everyone knew it was a Leap Year, being 4 years after 1996? When I lived in Brazil, everyone referred to Leap Year as bissextile. What was that all about? After the Gregorian reform in 1582, how come George Washington’s mother recorded his birth in their family bible as 11 February 1731 when we say it is 22 February 1732 (whereas Abraham Lincoln’s mother recorded 12 February 1809 for her son, which we agree with)? See
Being born on February 29 I have always had an interest in the calendar and the mechanics of Leap Year. Since I am sure everyone knows about Leap Year, I will just rattle off a few trivia questions to stimulate the memory. Why was I excited about my birthday in 2000 when everyone knew it was a Leap Year, being 4 years after 1996? When I lived in Brazil, everyone referred to Leap Year as bissextile. What was that all about? After the Gregorian reform in 1582, how come George Washington’s mother recorded his birth in their family bible as 11 February 1731 when we say it is 22 February 1732 (whereas Abraham Lincoln’s mother recorded 12 February 1809 for her son, which we agree with)? See  Tanya Khovanova’s recent blog post “The Annoyance of Hyperbolic Surfaces” about crocheting a hyperbolic surface added to the numerous examples of such activity, usually from knitting. Somehow this post caught my attention, in particular about the exponential growth of each added row and the fact that the resulting “surface” had constant negative curvature. I explored the exponential growth in this article and saved the mathematical exploration of the constant negative curvature for a later essay. See
Tanya Khovanova’s recent blog post “The Annoyance of Hyperbolic Surfaces” about crocheting a hyperbolic surface added to the numerous examples of such activity, usually from knitting. Somehow this post caught my attention, in particular about the exponential growth of each added row and the fact that the resulting “surface” had constant negative curvature. I explored the exponential growth in this article and saved the mathematical exploration of the constant negative curvature for a later essay. See  This article is basically a technical footnote without wider significance. At the time I had been reading with interest Paul J. Nahin’s latest book Number-Crunching (2011). Nahin presents a problem that he will solve with the Monte Carlo sampling approach.
This article is basically a technical footnote without wider significance. At the time I had been reading with interest Paul J. Nahin’s latest book Number-Crunching (2011). Nahin presents a problem that he will solve with the Monte Carlo sampling approach.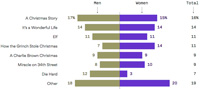 Reading Axios on Christmas Eve day 2017, I was struck by what appeared at first to be a strange graph showing preferences for Christmas movies divided between men and women. The thing that struck me as strange was the computation for the total votes: the percentages were the average of the men and women percentages. This, of course, is not how you average percentages. What was going on? See
Reading Axios on Christmas Eve day 2017, I was struck by what appeared at first to be a strange graph showing preferences for Christmas movies divided between men and women. The thing that struck me as strange was the computation for the total votes: the percentages were the average of the men and women percentages. This, of course, is not how you average percentages. What was going on? See