Tag Archives: complex numbers

Neuberg’s Theorem

This turned out to be a challenging puzzle from the 1980 Canadian Math Society’s magazine, Crux Mathematicorum.

“Proposed by Leon Bankoff, Los Angeles, California.

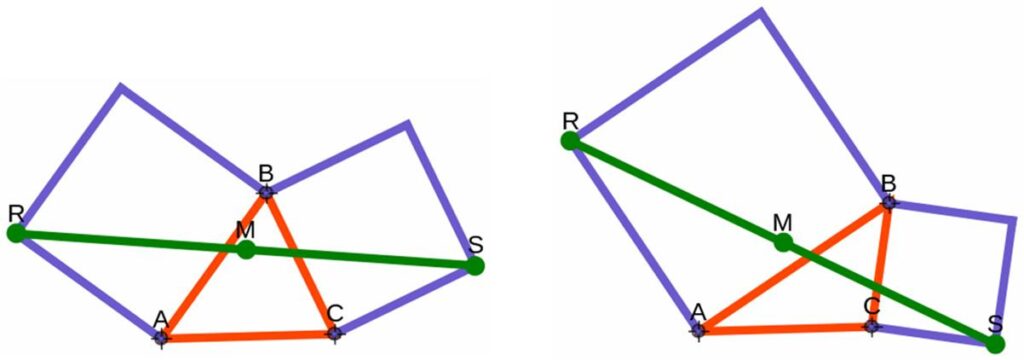
Professor Euclide Paracelso Bombasto Umbugio has once again retired to his tour d’ivoire where he is now delving into the supersophisticated intricacies of the works of Grassmann, as elucidated by Forder’s Calculus of Extension. His goal is to prove Neuberg’s Theorem:

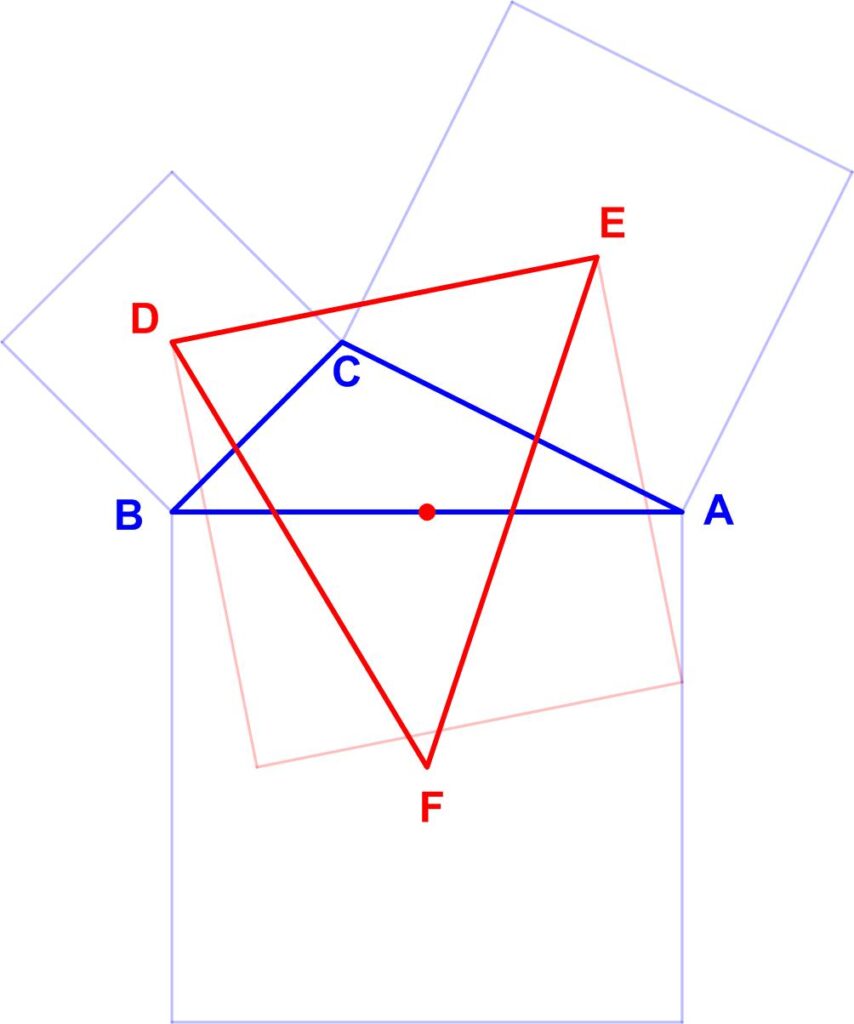
If D, E, F are the centers of squares described externally on the sides of a triangle ABC, then the midpoints of these sides are the centers of squares described internally on the sides of triangle DEF.  [The accompanying diagram shows only one internally described square.]

Help the dedicated professor emerge from his self-imposed confinement and enjoy the thrill of hyperventilation by showing how to solve his problem using only highschool, synthetic, Euclidean, ‘plain’ geometry.”

Alas, my plane geometry capability was inadequate to solve the puzzle that way, so I had to resort to the sledge hammer of analytic geometry, trigonometry, and complex variables.

See Neuberg’s Theorem

Bottema’s Theorem

This seemingly magical result from Futility Closet defies proof at first.  Go to the Wolfram demo by Jay Warendorff and then …

“Grab point B above and drag it to a new location. Surprisingly, M, the midpoint of RS, doesn’t move.

This works for any triangle — draw squares on two of its sides, note their common vertex, and draw a line that connects the vertices of the respective squares that lie opposite that point. Now changing the location of the common vertex does not change the location of the midpoint of the line.

It was discovered by Dutch mathematician Oene Bottema.”

As we shall see, Bottema’s Theorem has shown up in other guises as well.

See Bottema’s Theorem

A Self-Characterizing Figure

Futility Closet describes a result that is startling, amazing, and mysterious.

“This is pretty: If you choose n > 1 equally spaced points on a unit circle and connect one of them to each of the others, the product of the lengths of these chords equals n.”

The Futility Closet posting includes an interactive display using Wolfram Technology by Jay Warendorff that let’s you select different n and see the results.  It also includes a reference to a paper that proves the result; only the paper uses residue theory from complex variables, which seems a bit over-kill, though slick, for such a problem.  I found a simpler route.

See a Self-Characterizing Figure

Complex Numbers – Geometric Viewpoint

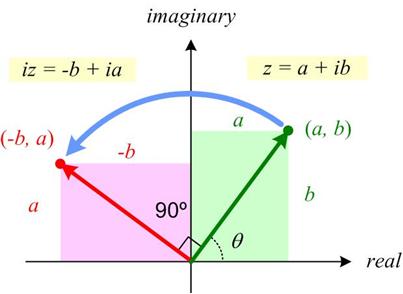This may be a futile attempt at an elementary introduction to complex variables by emphasizing their geometric properties. The elementary part is probably undermined by an initial discussion of field extensions and a necessary reference to trigonometry. Hopefully, the suppression of the explicit use of complex powers of Euler’s constant e until the very end will allow the geometric ideas to have center stage. A primary goal of the essay is to realize that complex polynomials involve sums of circles in the plane. The image of real polynomials as wavy curves in the plane is misleading for an understanding of complex behavior. See Complex Numbers – Geometric Viewpoint.