Here is a fairly computationally challenging 1994 AIME problem .
“Find the positive integer n for which
⌊log2 1⌋ + ⌊log2 2⌋ + ⌊log2 3⌋ + … + ⌊log2 n⌋ = 1994.
where for real x, ⌊x⌋ is the greatest integer ≤ x.”
There is some fussy consideration of indices.
See the Special Log Sum for a solution.
Well, I discovered that the 2024 Math Calendar has some interesting problems, so I guess things will limp along for a while. This is a challenging but imaginative problem from the calendar.
_______________
As before, recall that all the answers are integer days of the month.
See the Amazing Root Problem for a solution.
This is yet another series offered by Presh Talwalkar.
“What is the value of the following sum?
____
Talwalkar gives hints for three possible approaches to the solution.
See Another Challenging Sum for solutions.
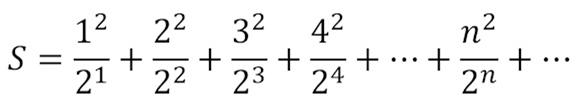
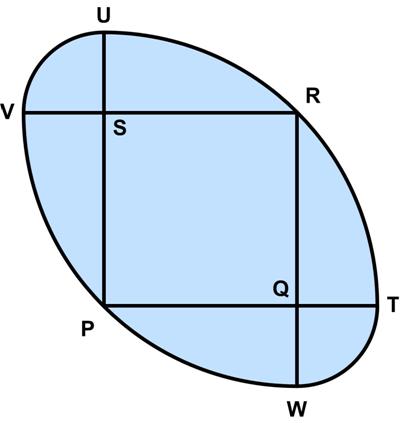Here is another UKMT Senior Challenge problem for 2017.
“The diagram shows a square PQRS with edges of length 1, and four arcs, each of which is a quarter of a circle. Arc TRU has centre P; arc VPW has centre R; arc UV has centre S; and arc WT has centre Q.
What is the length of the perimeter of the shaded region?
A_6___B_(2√2 – 1)π___C_(√2 – 1/2)π ___D_2___E_(3√2 – 2)π”
See Elliptic Circles for a solution.
This is a most surprising and amazing identity from the 1965 Polish Mathematical Olympiads.
“31. Prove that if n is a natural number, then we have
(√2 – 1)n = √m – √(m – 1),
where m is a natural number.”
Here, natural numbers are 1, 2, 3, …
I found it to be quite challenging, as all the Polish Math Olympiad problems seem to be.
See the Amazing Identity
Here is another challenging problem from the Polish Mathematical Olympiads. Its generality will cause more thought than for a simpler, specific problem.
“A cyclist sets off from point O and rides with constant velocity v along a rectilinear highway. A messenger, who is at a distance a from point O and at a distance b from the highway, wants to deliver a letter to the cyclist. What is the minimum velocity with which the messenger should run in order to attain his objective?”
See the Tired Messenger Problem
Here is another typical sum puzzle from Presh Talwalkar.
“Solve the following sums:
_____1/(1×3) + 1/(3×5) + 1/(5×7) + 1/(7×9) + 1/(9×11) =
_____1/(4×7) + 1/(7×10) + 1/(10×13) + 1/(13×16) =
_____1/(2×7) + 1/(7×12) + 1/(12×17) + … =”
The only reason I am including this puzzle is that Talwalkar gets very excited about deriving a formula that can solve sums of this type. This gives me an opportunity to discuss the “formula vs. procedure” way of doing math.
See the Incredible Trick Puzzle for solutions.
This is another physics-based problem from Colin Hughes’s Maths Challenge website (mathschallenge.net) that may take a bit more thought.
“A firework rocket is fired vertically upwards with a constant acceleration of 4 m/s2 until the chemical fuel expires. Its ascent is then slowed by gravity until it reaches a maximum height of 138 metres.
Assuming no air resistance and taking g = 9.8 m/s2, how long does it take to reach its maximum height?”
I can never remember the formulas relating acceleration, velocity, and distance, so I always derive them via integration.
See the Fireworks Rocket for solutions.
This is another stimulating little problem from the 2022 Math Calendar.
“a1 = 1, a2 = 2, …, an+1 = an + 6an-1
x = lim an+1/an as n → ∞
Solve for x.”
As before, recall that all the answers are integer days of the month.
See Stimulating Sequence for a solution.
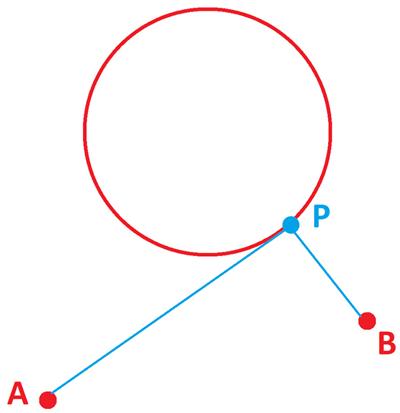James Tanton provides another imaginative problem on Twitter.
“I am at point A and want to walk to point B via some point, any point, P on the circle. What point P should I choose so that my journey A → P → B is as short as possible?”
Hint: I got ideas for a solution from two of my posts, “Square Root Minimum” and “Maximum Product”.
