Author Archives: Jim Stevenson

Train Wreck Puzzle

I thought it might be interesting to explore the mathematics of a common problem with a store-bought HO model train set that contains a collection of straight track segments and fixed-radius curved track segments that form a simple oval.  Invariably an initial run of the train has it careening off the track when the train first meets the curved segment after running along the straight track segments.

Why is that?  Well of course the train is going too fast.  But even if it slows down enough not to fall off the curve, it still jerks unstably and may derail when it first reaches the beginning of the curve.  What is going on?

See the Train Wreck Puzzle

(Updates 9/18/2022, 10/20/2022)  Others on Circular Looping Roller Coasters Continue reading →

Three Runners Puzzle

Here is another problem from Presh Talwalkar which he says is adapted from India’s Civil Services Exam.

“There are three runners X, Y, and Z. Each runs with a different uniform speed in a 1000 meters race.  If X gives Y a start of 50 meters, they will finish the race at the same time.  If X gives Z a start of 69 meters, they will finish the race at the same time.  Suppose Y and Z are in a [1000 meter] race. How much of a start should Y give to Z so they would finish the race at the same time?”

Even though Talwalkar’s original graphic showed all the runners in a 1000 meter race, it was not immediately clear to me from the wording that the race between Y and Z was also 1000 meters.  But that was the case, so I made it explicit.

Answer.

See the Three Runners Puzzle for solutions.

Rock, Paper, Scissors Problem

Here is another problem from the Sherlock Holmes puzzle book by Dr. Watson (aka Tim Dedopulos).

“Wiggins grinned at me. ‘You’ve not played Rock Paper Scissors before, Doctor?’

‘Doesn’t ring a bell,’ I told him.

‘Two of you randomly pick one of the three, and shout your choice simultaneously. There are hand gestures, too. If you both get the same, it’s a draw. Otherwise, scissors beats paper, paper beats rock, and rock beats scissors.’

‘So it’s a way of settling an argument,’ I suggested.

‘You were brought up wrong, Doctor,’ Wiggins said gravely. ‘Look, try it this way. I played a series of ten games with Alice earlier. I picked scissors six times, rock three times, and paper once. She picked scissors four times, rock twice, and paper four times. None of our games were drawn.’ He glanced at Holmes, who nodded. ‘So then, Doctor. What was the overall score for the series?’ ”

Answer.

See the Rock Paper Scissors Problem for solutions.

(Update 7/29/2021)  This problem in a different guise was presented by Futility Closet (7/28/2021) and attributed to Yoshinao Katagiri in Nobuyuki Yoshigahara’s Puzzles 101: A Puzzlemaster’s Challenge, 2004.

Passion Kiss Problem

This is a somewhat challenging math cryptogram in a slightly different guise from the Canadian Math Society’s magazine, Crux Mathematicorum.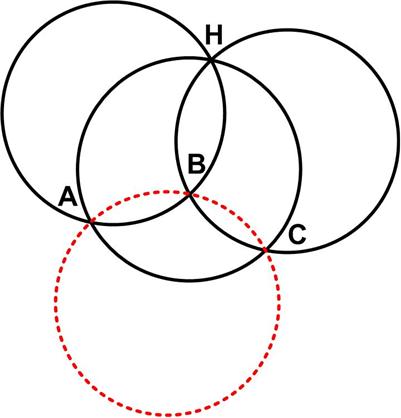

“But you can’t make arithmetic out of passion. Passion has no square root.” (Steve Shagan, City of Angels, G.P. Putnam’s Sons, New York, 1975, p. 16.)

On the contrary, show that in the decimal system

has a unique solution.

Answer.

See the Passion Kiss Problem for solutions.

Three Equal Circles

Here is a problem from the Quantum magazine, only this time from the “Challenges” section (these are expected to be a bit more difficult than the Brainteasers).

“Three circles with the same radius r all pass through a point H.  Prove that the circle passing through the points where the pairs of circles intersect (that is, points A, B, and C) also has the same radius r.”

Indeed, I found this quite challenging.  It took me several weeks to work out my approach and details.

See Three Equal Circles

Diabolical Triangle Puzzle

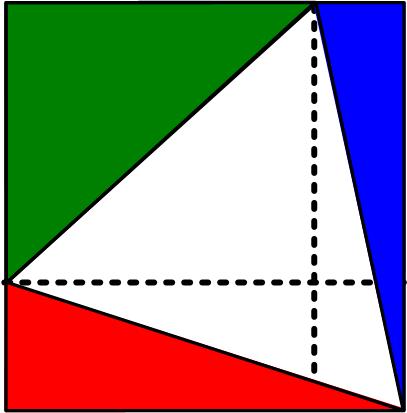This simple-appearing problem is from the 17 August 2020 MathsMonday offering by MEI, an independent curriculum development body for mathematics education in the UK.

“The diagram shows an equilateral triangle in a rectangle.  The two shapes share a corner and the other corners of the triangle lie on the edges of the rectangle.  Prove that the area of the green triangle is equal to the sum of the areas of the blue and red triangles.  What is the most elegant proof of this fact?”

Since the MEI twitter page seemed to be aimed at the high school level and the parting challenge seemed to indicate that there was one of those simple, revealing solutions to the problem, I spent several days trying to find one.  I went down a number of rabbit holes and kept arriving at circular reasoning results that assumed what I wanted to prove.  Visio revealed a number of fascinating relationships, but they all assumed the result and did not provide a proof.  I finally found an approach that I thought was at least semi-elegant.

See the Diabolical Triangle Puzzle

(Update 1/30/2021)  New MEI Solution

Twin Intersection Puzzle

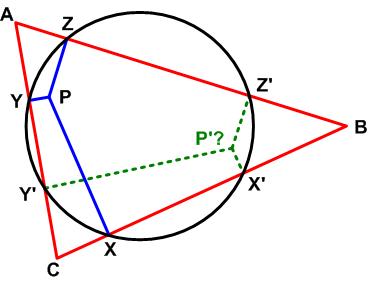This is an interesting problem from the 1977 Canadian Math Society’s magazine, Crux Mathematicorum.

“206. [1977: 10] Proposed by Dan Pedoe, University of Minnesota.

A circle intersects the sides BC, CA and AB of a triangle ABC in the pairs of points X, X’, Y, Y’ and Z, Z’ respectively. If the perpendiculars at X, Y and Z to the respective sides BC, CA and AB are concurrent at a point P, prove that the respective perpendiculars at X’, Y’ and Z’ to the sides BC, CA and AB are concurrent at a point P’.”

See the Twin Intersection Puzzle

Puzzles and Problems: plane geometry, Dan Pedoe, Crux Mathematicorum

Pole Leveling Puzzle

This is another thoughtful puzzle from the imaginative mind of James Tanton (with slight edits).

“Three poles of height 1183 feet, 182 feet, 637 feet stand in the ground. Pick a pole and saw off all the taller poles at that height. Plant those tops in the ground too. Repeat until no more such saw cuts can be made. Despite choices made along the way, what final result is sure to occur? [Four poles, heights a, b, c, d ft?]”

Answer.

See the Pole Leveling Puzzle for a solution.

  1. Pages:
  3. 1
  4. ...
  5. 23
  6. 24
  7. 25
  8. 26
  9. 27
  10. 28
  11. 29
  12. ...
  13. 47