 This is a slightly challenging problem from BL’s Math Games.
This is a slightly challenging problem from BL’s Math Games.
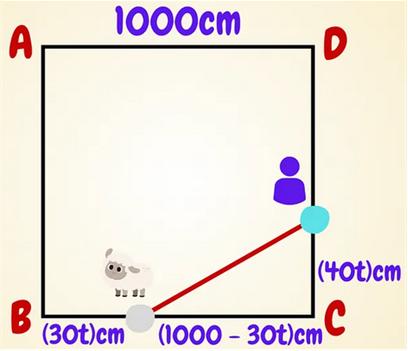
“In a square garden ABCD of side 10m, a sheep sets off from B and moves along BC at 30cm per minute. At the same time, you set off from C and move along edge CD at 40cm per minute. The question is, what’s the shortest distance between you and the sheep in meters?
This is somewhat an optimization problem because as you and the sheep move along the sides of the square at different rates, the distance in between varies as you can imagine.”
There’s at least one non-calculus solution and of course one calculus solution.
See Sheep in Garden Problem for solutions.

 I came across this remarkable
I came across this remarkable  I came across an interesting problem in the MathsJam Shout for February 2022.
I came across an interesting problem in the MathsJam Shout for February 2022.
 Here is another challenging problem from the first issue of the 1874 The Analyst, which also appears in Benjamin Wardhaugh’s book.
Here is another challenging problem from the first issue of the 1874 The Analyst, which also appears in Benjamin Wardhaugh’s book.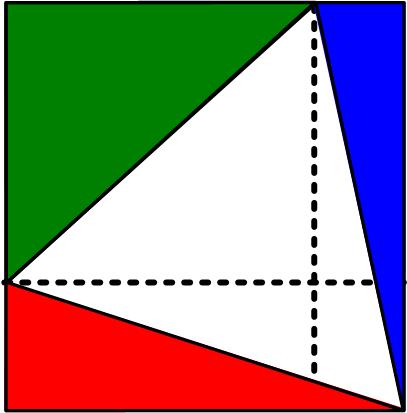 This simple-appearing problem is from the 17 August 2020 MathsMonday
This simple-appearing problem is from the 17 August 2020 MathsMonday  This is a stimulating problem from the UKMT Senior Math Challenge for 2017. The additional problem “for investigation” is particularly challenging. (I have edited the problem slightly for clarity.)
This is a stimulating problem from the UKMT Senior Math Challenge for 2017. The additional problem “for investigation” is particularly challenging. (I have edited the problem slightly for clarity.) This is from the UKMT Senior Challenge of 2004.
This is from the UKMT Senior Challenge of 2004.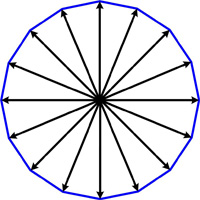 This is a fun problem from Mathematical Quickies (1967).
This is a fun problem from Mathematical Quickies (1967).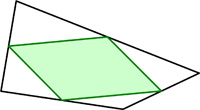 I came across this problem in Alfred Posamentier’s book, but I remember I had seen it a couple of places before and had never thought to solve it. At first, it seems like magic.
I came across this problem in Alfred Posamentier’s book, but I remember I had seen it a couple of places before and had never thought to solve it. At first, it seems like magic.