 This is a slightly challenging problem from BL’s Math Games.
This is a slightly challenging problem from BL’s Math Games.
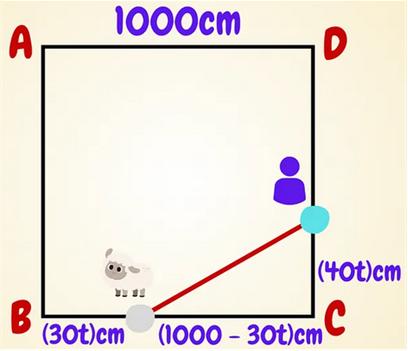
“In a square garden ABCD of side 10m, a sheep sets off from B and moves along BC at 30cm per minute. At the same time, you set off from C and move along edge CD at 40cm per minute. The question is, what’s the shortest distance between you and the sheep in meters?
This is somewhat an optimization problem because as you and the sheep move along the sides of the square at different rates, the distance in between varies as you can imagine.”
There’s at least one non-calculus solution and of course one calculus solution.
See Sheep in Garden Problem for solutions.

 This is a
This is a  This is another nice problem from the 2025 Math Calendar.
This is another nice problem from the 2025 Math Calendar.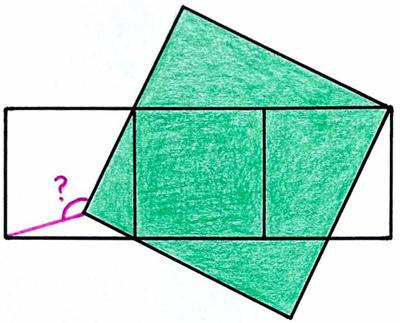 This is another Catriona Agg
This is another Catriona Agg  This is another take on the passing train type puzzle from the Moscow Puzzles.
This is another take on the passing train type puzzle from the Moscow Puzzles. I have been meaning to focus on this aspect of mathematics for some time. It is a topic I elaborated in my “Angular Momentum”
I have been meaning to focus on this aspect of mathematics for some time. It is a topic I elaborated in my “Angular Momentum”  This is a lovely
This is a lovely 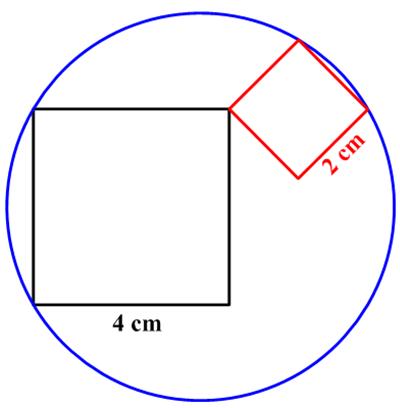 This
This  Here is a probability
Here is a probability  This is another
This is another