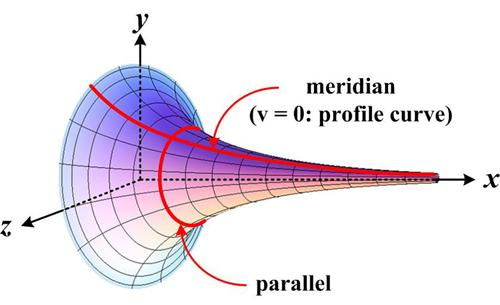
This essay began as an effort to prove Tanya Khovanova’s statement in her article “The Annoyance of Hyperbolic Surfaces” that her crocheted hyperbolic surface had constant (negative) curvature. I discussed Khovanova’s article in my previous essay “Exponential Yarn”. What I thought would be a fairly straight-forward exercise turned into a more concerted effort as I concluded that her crocheted surface did not have constant curvature. However, I found additional references that supported her statement, so I was becoming quite confused. I looked at other, similar surfaces to try to understand the whole curvature situation. This involved a lot of tedious computations (with my usual plethora of mistakes) that proved most challenging. But then I realized where I had gone astray. To cover my ignorance I claimed my error stemmed from a subtle misunderstanding. Herewith is a presentation of what I found. See Bugles, Trumpets, and Beltrami.

(Update 4/6/2019)I made a cosmetic change to the presentation of the hyperbola function h(u) = 1/u curvature in order to make it compatible with the discussions of the exponential and tractrix curvatures, namely, I expressed the equations and figures in terms of h instead of u.