 This is another delightful H. E. Dudeney puzzle.
This is another delightful H. E. Dudeney puzzle.
“Mr. Gubbins, a diligent man of business, was much inconvenienced by a London fog. The electric light happened to be out of order and he had to manage as best he could with two candles. His clerk assured him that though both were of the same length one candle would burn for four hours and the other for five hours. After he had been working some time he put the candles out as the fog had lifted, and he then noticed that what remained of one candle was exactly four times the length of what was left of the other.
When he got home that night Mr. Gubbins, who liked a good puzzle, said to himself, ‘Of course it is possible to work out just how long those two candles were burning to-day. I’ll have a shot at it.’ But he soon found himself in a worse fog than the atmospheric one. Could you have assisted him in his dilemma? How long were the candles burning?”
See Mr. Gubbins in a Fog for a solution.

 In a June Chalkdust
In a June Chalkdust 
 This is a great
This is a great  This is a tricky product problem from Alfred Posamentier which naturally has a slick solution—if you can think of it.
This is a tricky product problem from Alfred Posamentier which naturally has a slick solution—if you can think of it.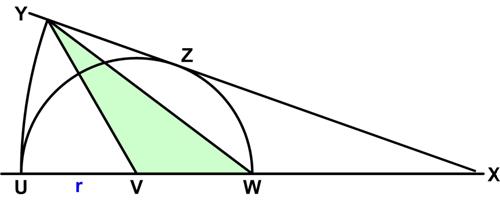 Here is a problem from the UKMT Senior (17-18 year-old) Mathematics Challenge for 2012:
Here is a problem from the UKMT Senior (17-18 year-old) Mathematics Challenge for 2012: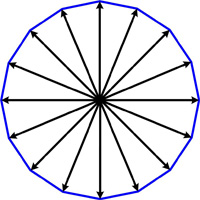 This is a fun problem from Mathematical Quickies (1967).
This is a fun problem from Mathematical Quickies (1967).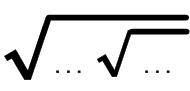 This is another UKMT Senior Challenge problem, but for the year 2005. I thought it was diabolical and hadn’t a clue how to solve it. Even after reading the solution, I don’t think I could have come up with it. I take my hat off to anyone who solves it.
This is another UKMT Senior Challenge problem, but for the year 2005. I thought it was diabolical and hadn’t a clue how to solve it. Even after reading the solution, I don’t think I could have come up with it. I take my hat off to anyone who solves it.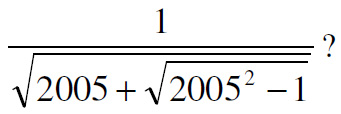
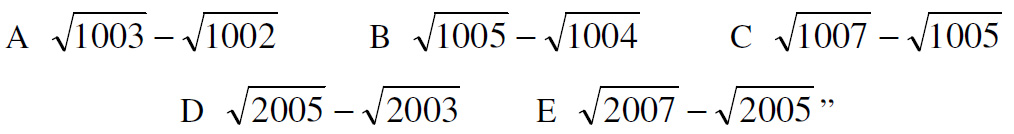
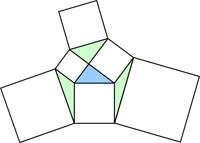 This is a problem from the UKMT Senior Challenge for 2001. (It has been slightly edited to reflect the colors I added to the diagram.)
This is a problem from the UKMT Senior Challenge for 2001. (It has been slightly edited to reflect the colors I added to the diagram.) Yet another train problem from H. E. Dudeney.
Yet another train problem from H. E. Dudeney.