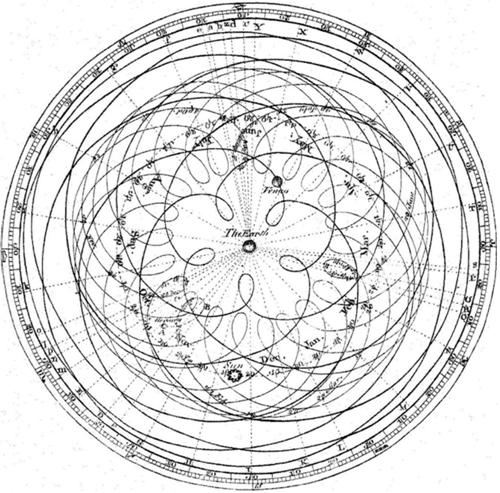
 Given the aggravating times, I thought I would vent my frustration by ranting on a somewhat nonsensical topic: “The fact that the earth revolves around the sun, rather than the sun around the earth.” This assertion is often used to separate the supposed dunces from the enlightened. It is put on the same level as “the fact that the earth is round (a sphere) and not flat” with the dunces labeled “flat-earthers.”
Given the aggravating times, I thought I would vent my frustration by ranting on a somewhat nonsensical topic: “The fact that the earth revolves around the sun, rather than the sun around the earth.” This assertion is often used to separate the supposed dunces from the enlightened. It is put on the same level as “the fact that the earth is round (a sphere) and not flat” with the dunces labeled “flat-earthers.”
However, I take umbrage with the use of the word “fact” to conflate these two instances as examples of what “is” or what is “true.” I claim the earth is spherical (more or less: a better approximation is an oblate spheroid) or certainly “curved” rather than “flat.” Whereas the statement that the “sun is at the center of the solar system” is not a fact but an arbitrary convenience.

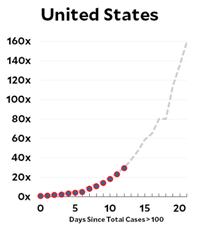 Given the mathematical nature of this website I feel reluctantly impelled to address the coronavirus pandemic. The mathematics behind the spread of infection is basically the same exponential growth that I discussed in the “
Given the mathematical nature of this website I feel reluctantly impelled to address the coronavirus pandemic. The mathematics behind the spread of infection is basically the same exponential growth that I discussed in the “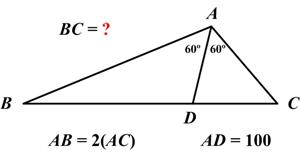 This is another problem from the indefatigable Presh Talwalkar.
This is another problem from the indefatigable Presh Talwalkar.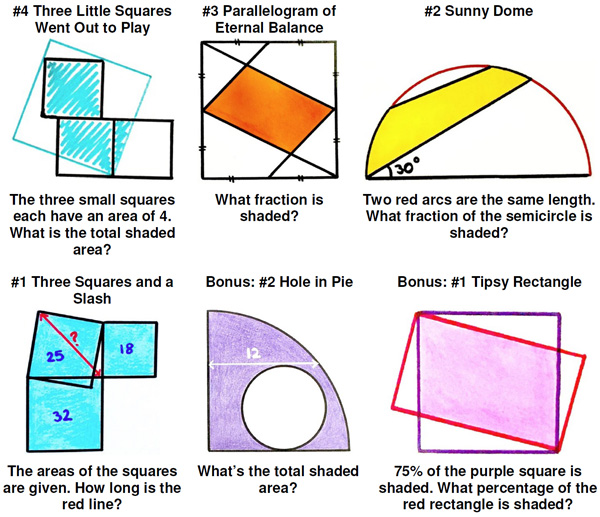
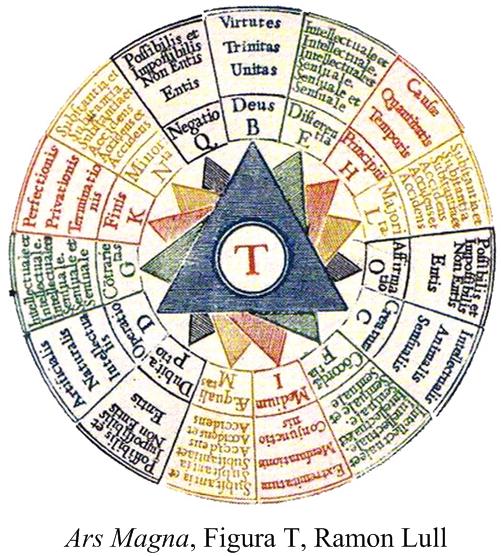 The subtext of this essay might be “word problems,” since the stream of thoughts that led to the za’irajah (zairja) began with a paper I read, while searching for potential problems for this website, on the history of word problems in high school texts in algebra in the 20th and 21st centuries. The following statement by Lorenat caught my attention:
The subtext of this essay might be “word problems,” since the stream of thoughts that led to the za’irajah (zairja) began with a paper I read, while searching for potential problems for this website, on the history of word problems in high school texts in algebra in the 20th and 21st centuries. The following statement by Lorenat caught my attention: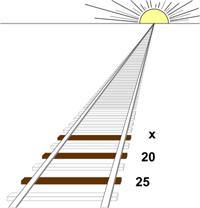 This is a surprisingly challenging puzzle from the Mathematics 2020 calendar.
This is a surprisingly challenging puzzle from the Mathematics 2020 calendar. The following problem from Five Hundred Mathematical Challenges was a challenge indeed, even though it appeared to be a standard travel puzzle.
The following problem from Five Hundred Mathematical Challenges was a challenge indeed, even though it appeared to be a standard travel puzzle.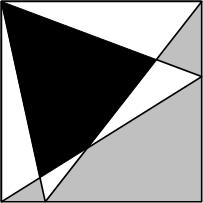 This is a problem from a while back (2015) at Futility Closet.
This is a problem from a while back (2015) at Futility Closet.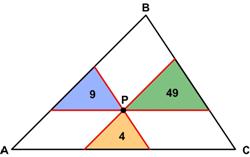 Here is another engaging problem from
Here is another engaging problem from  Here is another challenging problem from the 2004 Pi in the Sky Canadian magazine for high school students.
Here is another challenging problem from the 2004 Pi in the Sky Canadian magazine for high school students.