 I thought it would be interesting to present a recent entry in the mathematician John Baez’s Diary on some extremes in mathematics from the Bourbaki school, namely, how many symbols it would take to define the number “1.”
I thought it would be interesting to present a recent entry in the mathematician John Baez’s Diary on some extremes in mathematics from the Bourbaki school, namely, how many symbols it would take to define the number “1.”
I don’t know if the “mathematician” Nicolas Bourbaki holds any significance for students today, but in my time (math graduate school in the 1960s) the Bourbaki approach seemed to permeate everything.
My first exposure to Bourbaki was as a humorous figure described by Paul Halmos in his 1957 article in the Scientific American—the humor being that Bourbaki did not exist. As Halmos wrote:
“One of the legends surrounding the name is that about 25 or 30 years ago first-year students at the Ecole Normale Superieure (where most French mathematicians get their training) were annually exposed to a lecture by a distinguished visitor named Nicolas Bourbaki, who was in fact an amateur actor disguised in a patriarchal beard, and whose lecture was a masterful piece of mathematical double-talk. It is necessary to insert a word of warning about the unreliability of most Bourbaki stories. While the members of this cryptic organization have taken no blood oath of secrecy, most of them are so amused by their own joke that their stories about themselves are intentionally conflicting and apocryphal.”
Nicholas Bourbaki was the pseudonym for a group of French mathematicians who wished to write a treatise which would be, as Halmos stated, “a survey of all mathematics from a sophisticated point of view”.
See the Bourbaki World
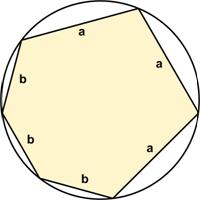 Here is another good problem from Five Hundred Mathematical Challenges:
Here is another good problem from Five Hundred Mathematical Challenges:
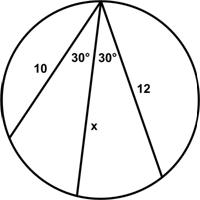 This is another challenging puzzle from
This is another challenging puzzle from  I thought it would be interesting to present a recent entry in the mathematician John Baez’s Diary on some extremes in mathematics from the Bourbaki school, namely, how many symbols it would take to define the number “1.”
I thought it would be interesting to present a recent entry in the mathematician John Baez’s Diary on some extremes in mathematics from the Bourbaki school, namely, how many symbols it would take to define the number “1.”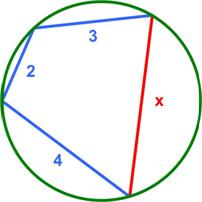
 Here is another problem from the 2020 Math Calendar to stimulate your mind.
Here is another problem from the 2020 Math Calendar to stimulate your mind. Here is another Brainteaser from the Quantum magazine.
Here is another Brainteaser from the Quantum magazine. In looking through some old files I came across a math magazine I had bought in 1998. It was called Quantum and was published by the National Science Teachers Association in collaboration with the Russian magazine Kvant during the period 1990 to 2001 (coinciding with the Russian thaw, which in the following age of Putin seems eons ago). Fortunately, they are all online now. Besides some fascinating math articles the magazine contains a column of “Brainteasers.” Here is one of them:
In looking through some old files I came across a math magazine I had bought in 1998. It was called Quantum and was published by the National Science Teachers Association in collaboration with the Russian magazine Kvant during the period 1990 to 2001 (coinciding with the Russian thaw, which in the following age of Putin seems eons ago). Fortunately, they are all online now. Besides some fascinating math articles the magazine contains a column of “Brainteasers.” Here is one of them: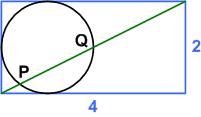 Here is another UKMT Senior Challenge problem from 2017, which has a straight-forward solution:
Here is another UKMT Senior Challenge problem from 2017, which has a straight-forward solution: A fun, relatively new, Sherlock Holmes puzzle book by Dr. Watson (aka Tim Dedopulos) has puzzles couched in terms of the Holmes-Watson banter. The following problem is a variation on the Sam Loyd
A fun, relatively new, Sherlock Holmes puzzle book by Dr. Watson (aka Tim Dedopulos) has puzzles couched in terms of the Holmes-Watson banter. The following problem is a variation on the Sam Loyd