This is a fairly straight-forward problem from the 1999 AIME problems.
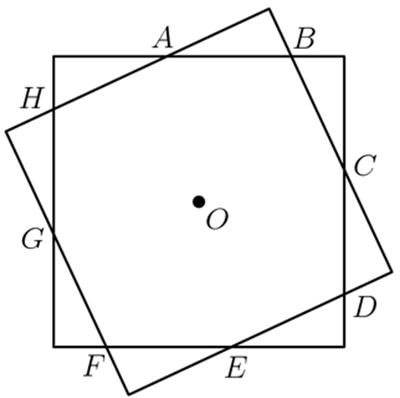
“The two squares shown share the same center O and have sides of length 1. The length of AB is 43/99 and the area of octagon ABCDEFGH is m/n where m and n are relatively prime positive integers. Find m + n.”
See the Another Octagonal Area Problem for solutions.
This is a clever puzzle from the 1986 AIME problems.
“The pages of a book are numbered 1 through n. When the page numbers of the book were added, one of the page numbers was mistakenly added twice, resulting in an incorrect sum of 1986. What was the number of the page that was added twice?”
See the Additional Page Problem for the solution.
Here is a fairly computationally challenging 1994 AIME problem .
“Find the positive integer n for which
⌊log2 1⌋ + ⌊log2 2⌋ + ⌊log2 3⌋ + … + ⌊log2 n⌋ = 1994.
where for real x, ⌊x⌋ is the greatest integer ≤ x.”
There is some fussy consideration of indices.
See the Special Log Sum for a solution.
This is a somewhat challenging problem from the 1997 American Invitational Mathematics Exam (AIME).
“A car travels due east at 2/3 miles per minute on a long, straight road. At the same time, a circular storm, whose radius is 51 miles, moves southeast at √2/2 miles per minute. At time t = 0, the center of the storm is 110 miles due north of the car. At time t = t1 minutes, the car enters the storm circle, and at time t = t2 minutes, the car leaves the storm circle. Find (t1 + t2)/2.”
See the Storm Chaser Problem for solutions.
This is a problem from the 1987 American Invitational Mathematics Exam (AIME).
“Al walks down to the bottom of an escalator that is moving up and he counts 150 steps. His friend, Bob, walks up to the top of the escalator and counts 75 steps. If Al’s speed of walking (in steps per unit time) is three times Bob’s walking speed, how many steps are visible on the escalator at a given time? (Assume that this value is constant.)”
See the Escalator Puzzle for solutions.
This is an initially mind-boggling problem from the 1995 American Invitational Mathematics Exam (AIME).
“Find the last three digits of the product of the positive roots of
”
See Log Lunacy for solution.
This is a fun problem from the 1989 American Invitational Mathematics Exam (AIME).
“Two skaters, Allie and Billie, are at points A and B, respectively, on a flat, frozen lake. The distance between A and B is 100 meters. Allie leaves A and skates at a speed of 8 meters per second on a straight line that makes a 60° angle with AB. At the same time Allie leaves A, Billie leaves B at a speed of 7 meters per second and follows the straight path that produces the earliest possible meeting of the two skaters, given their speeds. How many meters does Allie skate before meeting Billie?”
See the Skating Rendezvous Problem for solutions.
This is a slightly challenging problem from the 1993 American Invitational Mathematics Exam (AIME).
“Jenny and Kenny are walking in the same direction, Kenny at 3 feet per second and Jenny at 1 foot per second, on parallel paths that are 200 feet apart. A tall circular building 100 feet in diameter is centered midway between the paths. At the instant when the building first blocks the line of sight between Jenny and Kenny, they are 200 feet apart. Find t, the amount of time in seconds, before Jenny and Kenny can see each other again.”
See the Parallel Stroll Problem for solutions.
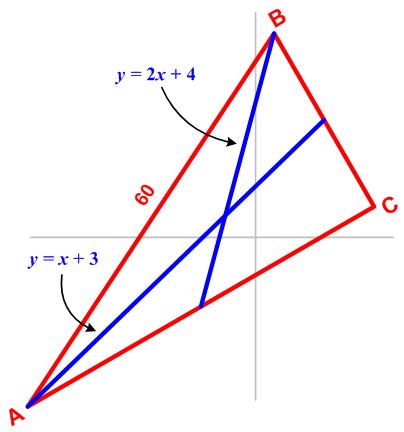This is a challenging problem from the 1986 American Invitational Mathematics Exam (AIME).
“Let triangle ABC be a right triangle in the xy-plane with a right angle at C. Given that the length of the hypotenuse AB is 60, and that the medians through A and B lie along the lines y = x + 3 and y = 2x + 4 respectively, find the area of triangle ABC.”
I have included a sketch to indicate that the sides of the right triangle are not parallel to the Cartesian coordinate axes.
The AIME (American Invitational Mathematics Examination) is an intermediate examination between the American Mathematics Competitions AMC 10 or AMC 12 and the USAMO (United States of America Mathematical Olympiad). All students who took the AMC 12 (high school 12th grade) and achieved a score of 100 or more out of a possible 150 or were in the top 5% are invited to take the AIME. All students who took the AMC 10 (high school 10th grade and below) and had a score of 120 or more out of a possible 150, or were in the top 2.5% also qualify for the AIME.
See the Challenging Triangle Problem for solutions.
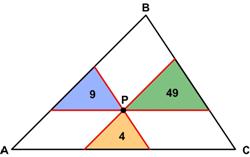Here is another engaging problem from Presh Talwalkar.
“___________Triangle Area 1984 AIME
Point P is in the interior of triangle ABC, and the lines through P are parallel to the sides of ABC. The three triangles shown in the diagram have areas of 4, 9, and 49. What is the area of triangle ABC?”
See the Pinwheel Area Problem. for solutions.
