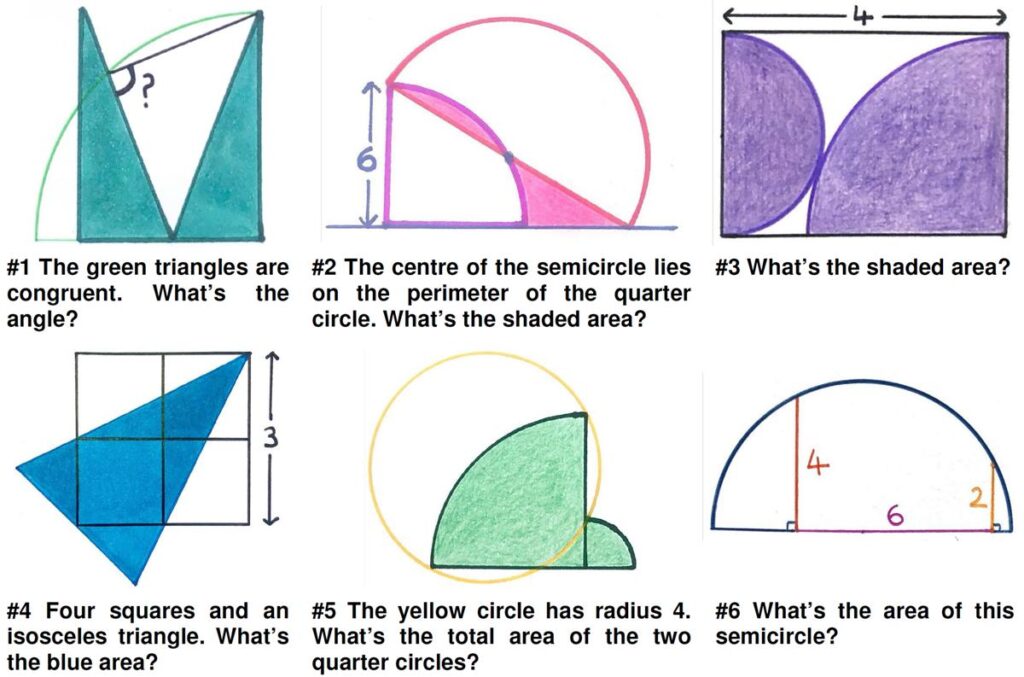
 This is a puzzle from the A+Click site.
This is a puzzle from the A+Click site.
“There is a fault with the cruise control on Hank’s car such that the speed continuously and linearly increases with time. When he starts off the speed is set to exactly 60 mph. He is driving on a long straight route with the radio on at full blast and he is not paying any attention to his speed. After 3 hours he notices that his speed has now reached 80 mph. For how many miles did he drive above the state speed limit of 70 mph?
Answer Choices: 125 miles 112.5 miles 105 miles 99.5 miles”
See Unlawful Distance for solutions.

 This is another nice problem from the 2025 Math Calendar.
This is another nice problem from the 2025 Math Calendar.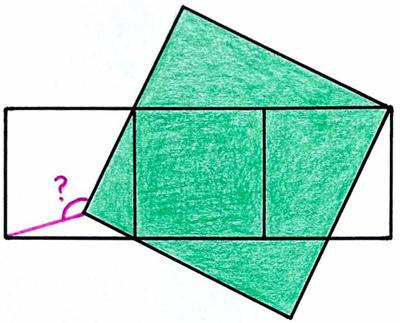 This is another Catriona Agg
This is another Catriona Agg  This is a lovely
This is a lovely 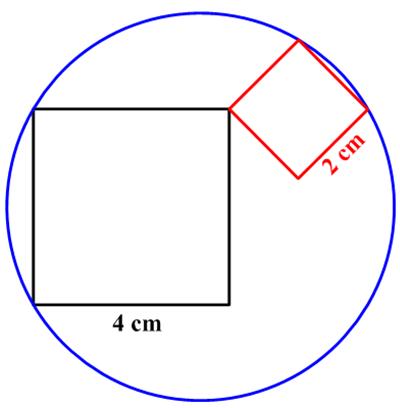 This
This 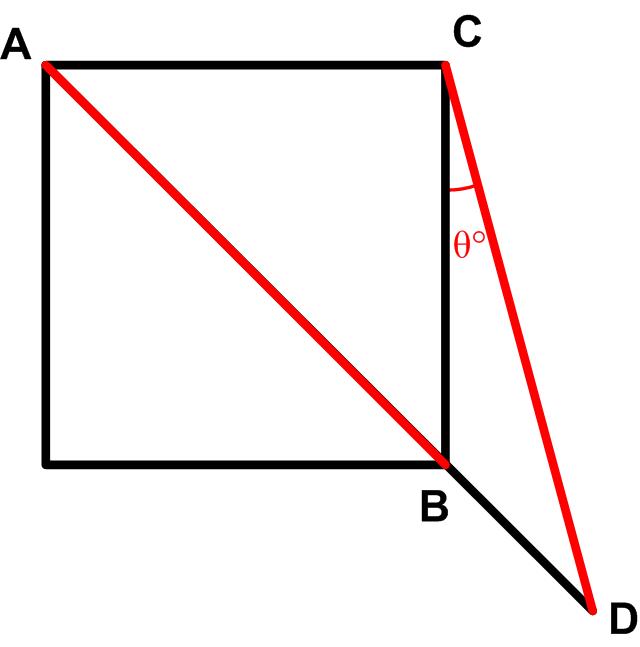 For me this turned out to be sort of a challenging problem from the 2025 Math Calendar.
For me this turned out to be sort of a challenging problem from the 2025 Math Calendar.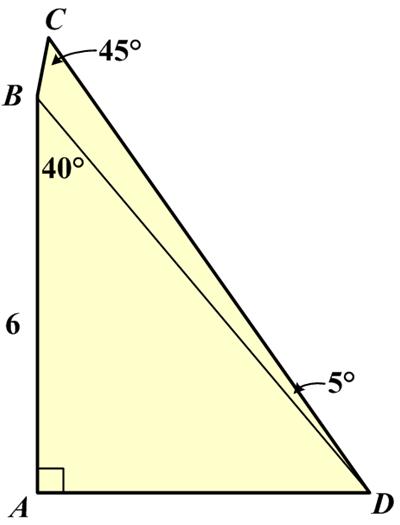 This is another intimidating
This is another intimidating  This is an interesting problem from the Canadian Mathematical Society’s 2001 Olymon.
This is an interesting problem from the Canadian Mathematical Society’s 2001 Olymon.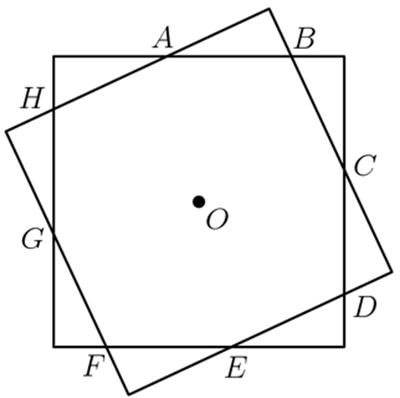 This is a fairly straight-forward problem from the 1999 AIME problems.
This is a fairly straight-forward problem from the 1999 AIME problems.