The following interesting behavior was found at the Futility Closet website:

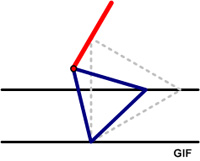
“A pleasing fact from David Wells’ Archimedes Mathematics Education Newsletter: Draw two parallel lines. Fix a point A on one line and move a second point B along the other line. If an equilateral triangle is constructed with these two points as two of its vertices, then as the second point moves, the third vertex C of the triangle will trace out a straight line. Thanks to reader Matthew Scroggs for the tip and the GIF.”

This is rather amazing and cries out for a proof. It also raises the question of how anyone noticed this behavior in the first place. I proved the result with calculus, but I wonder if there is a slicker way that makes it more obvious. See the Straight and Narrow Problem.

(Update 3/25/2019)In discovering that the David Wells of the “Regiomontanus 1471 Problem” was the same person referenced in the “Straight and Narrow” Futility Closet article, I was able to find the exact reference Futility Closet used, namely,

Wells, David, “An equilateral triangle on three parallel lines,” Archimedes Mathematics Education Newsletter, #1 January 04 2016, p.35 (https://drive.google.com/file/d/0BwT4tltuHZVdME0weEJLWWdlVGM/view, retrieved 3/25/2019)

In his article Wells provides the geometric argument I was wondering about. Rather than reproduce the discussion, I recommend referring to the original article, which has a much broader exploration of the matter. Ironically, I am reminded of the situation in Newton’s Principia where he uses plane geometric arguments in place of the calculus he so recently espoused. It may be a matter of taste which is preferable: geometry or calculus. I have to admit in both cases, Newton’s and the “Straight and Narrow Problem”, I prefer the calculus as simpler and more direct.