Here is another simply amazing problem from Five Hundred Mathematical Challenges:
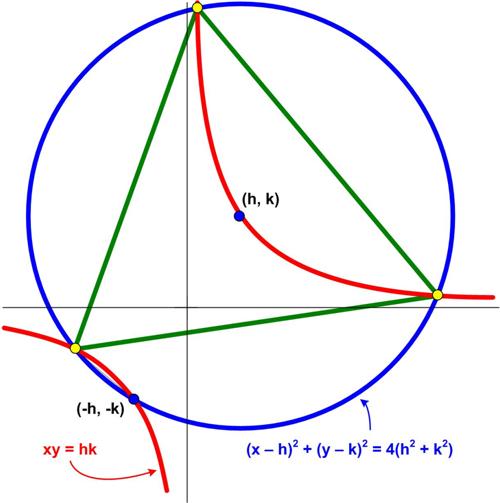
“Problem 154. Show that three solutions, (x1,.y1), (x2,.y2), (x3, y3), of the four solutions of the simultaneous equations
____________(x – h)² + (y – k)² = 4(h² + k²)
______________________xy = hk
are vertices of an equilateral triangle. Give a geometrical interpretation.”
Again, I don’t see how anyone could have discovered this property involving a circle, a hyperbola, and an equilateral triangle. It seems plausible when h.=.k, but it is not at all obvious for h.≠.k. For some reason, I had difficulty getting a start on a solution, until the obvious approach dawned on me. I don’t know why it took me so long.
See the Amazing Triangle Problem.
greetings dear Jim Stevenson,
I am writing to you regarding your excellent article which explains the relation between Zairja and mathematics, can you explain to me a paragraph of your article which I do not understand well: “The early symbolic algebra mathematical machine of 1600 transformed almost 5000 years o doing mathematical problems. Its results were so powerful, that within another 100 years it had been expanded to solve geometric problems (analytic geometry) and physical problems involving change and the infinite (calculus) “. Which machine are you talking about in this paragraph ?
Reda Naji (amateur historian)
I confess I was being a bit metaphorical here in the use of the word “machine.” The logic wheels of Ramon Lull could be thought of as a physical machine in that they supposedly could be rotated against each other to line up different permutations of terms and somehow yield answers to questions. The idea was that it was a “mechanical” procedure and did not involve direct human thought. This supposedly gave it an objective basis that would be more convincing than a subjective human argument. Similarly, having to reason about quantitative problems verbally may involve subjective techniques that may belong more to the modern arena of “mental math.” The point I was trying to make was with the advent of symbolic algebra (symbols and procedures for using constants, variables, unknowns, arithmetic operations, fractions, etc.) solving quantitative problems could be reduced to a mechanical procedure that did not require thinking other than how to apply rules (once a mathematical model had been determined!). Of course, and abacus was a real mechanical machine that could do arithmetic, but it couldn’t solve equations for an unknown. And the simple “mechanical” symbolic operations of addition, subtraction, multiplication, and division in algebra soon expanded to include the operations of differentiation and integration in calculus, building an even bigger and more powerful mathematical “machine.”
I see this comment came in under the Amazing Triangle Problem. It probably should be associated with The Za’irajah and Mathematics.