I found this problem from the 1981 Canadian Math Society’s magazine, Crux Mathematicorum, to be quite challenging.

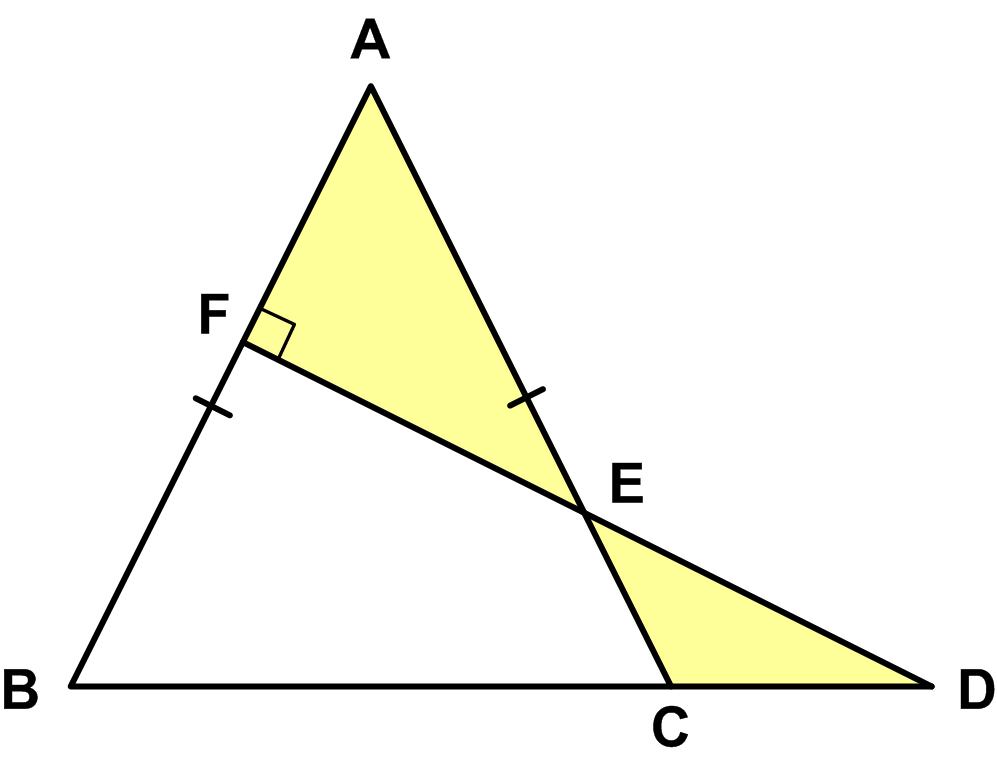
“Proposed by Kaidy Tan, Fukien Teachers’ University, Foochow, Fukien, China.

An isosceles triangle has vertex A and base BC. Through a point F on AB, a perpendicular to AB is drawn to meet AC in E and BC produced in D. Prove synthetically that

Area of AFE = 2 Area of CDE   if and only if  AF = CD.”

See the Linked Triangles Problem

(Update 2/22/2023, 6/9/2023) Alternative Solutions

(Update 2/22/2023)

The indefatigable Oscar Rojas has come up with an alternative solution to the problem. It takes a bit of study to verify.

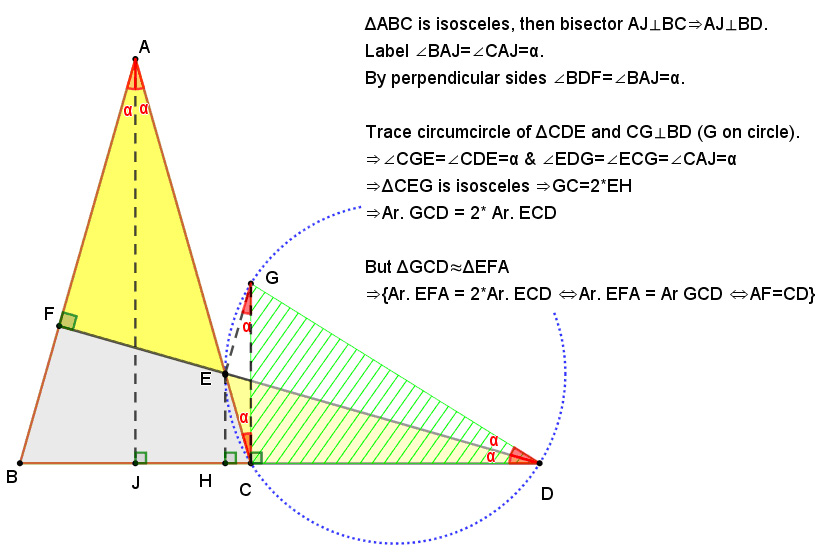
(Update 6/9/2023)

Srhiri Noe from Morocco, a former high school teacher and teacher trainer, has provided another solution to the problem.  I have edited the solution slightly for clarity.