
Here is a mind-numbing logic puzzle from Futility Closet.
“A puzzle by H.A. Thurston, from the April 1947 issue of Eureka, the journal of recreational mathematics published at Cambridge University:
Five people make the following statements:—

Which of these statements are true and which false? It will be found on trial that there is only one possibility. Thus, prove or disprove Fermat’s last theorem.”
Normally I would forgo something this complicated, but I thought I would give it a try. I was surprised that I was able to solve it, though it took some tedious work. (Hint: truth tables. See the “Pointing Fingers” post regarding truth tables.)
One important note. The author is a bit cavalier about the use of “Either …, or …”. In common parlance this means “either P is true or Q is true, but not both” (exclusive “or”: XOR), whereas in logic “or” means “either P is true or Q is true, or possibly both” (inclusive “or”: OR). I assumed all “Either …, or …” and “or” expressions were the logical inclusive “or”, which turned out to be the case.
See the Fermat’s Last Theorem Puzzle
 This is a lovely result from Futility Closet.
This is a lovely result from Futility Closet.
 Here is an entertaining
Here is an entertaining  This is a puzzle from
This is a puzzle from 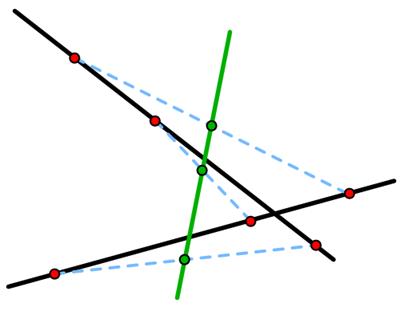 I came across this remarkable
I came across this remarkable 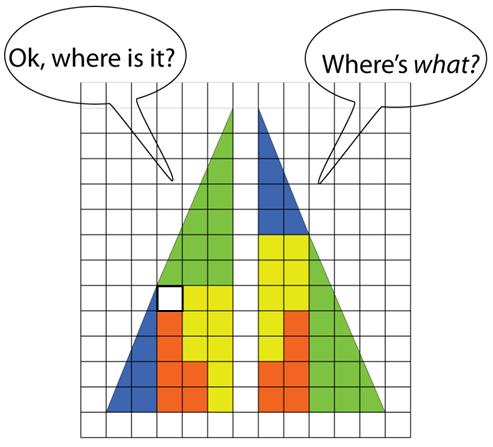 Coming across this
Coming across this  This is an intriguing
This is an intriguing 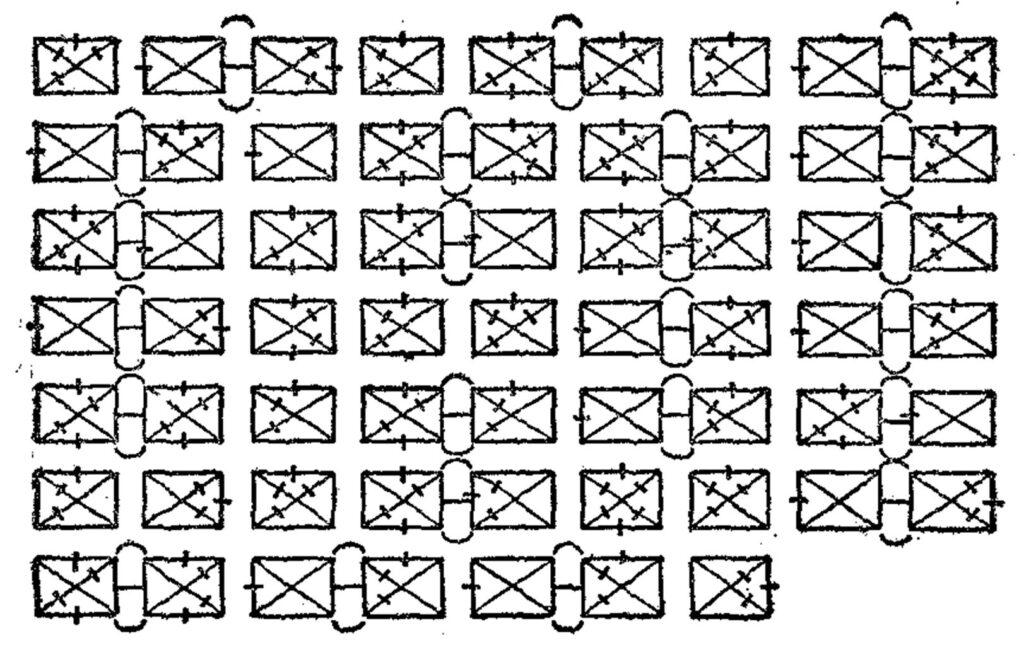
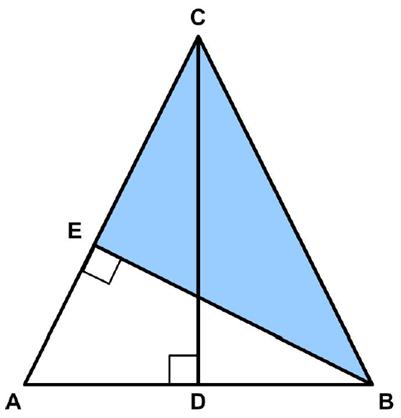 The Futility Closet website had the following
The Futility Closet website had the following 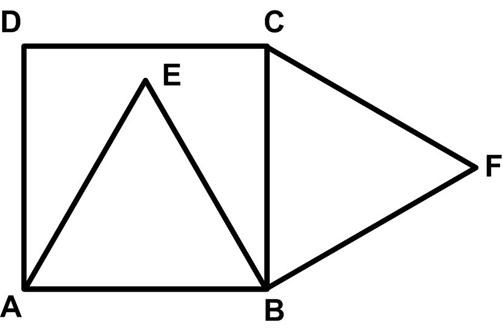 This is a fairly simple problem from
This is a fairly simple problem from 

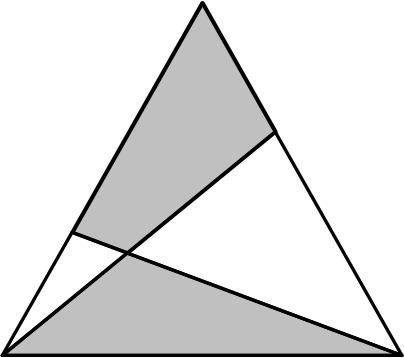 This is another fairly simple puzzle from Futility Closet from a while ago (2014).
This is another fairly simple puzzle from Futility Closet from a while ago (2014).