 Here is another Brainteaser from the Quantum magazine.
Here is another Brainteaser from the Quantum magazine.
“Mr. R. A. Scall, president of the Pyramid Bank, lives in a suburb rather far from his office. Every weekday a car from the bank comes to his house, always at the same time, so that he arrives at work precisely when the bank opens. One morning his driver called very early to tell him he would probably be late because of mechanical problems. So Mr. Scall left home one hour early and started walking to his office. The driver managed to fix the car quickly, however, and left the garage on time. He met the banker on the road and brought him to the bank. They arrived 20 minutes earlier than usual. How much time did Mr. Scall walk? (The car’s speed is constant, and the time needed to turn around is zero.) (I. Sharygin)”
I struggled with some of the ambiguities in the problem and made my own assumptions. But it turned out there was a reason they were ambiguous.
Answer.
See the Walking Banker Problem for solutions.
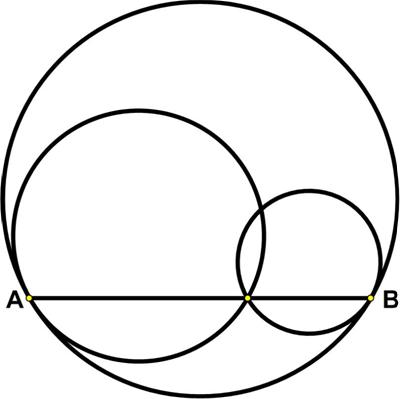 Here is another problem from the “Challenges” section of the Quantum magazine.
Here is another problem from the “Challenges” section of the Quantum magazine.
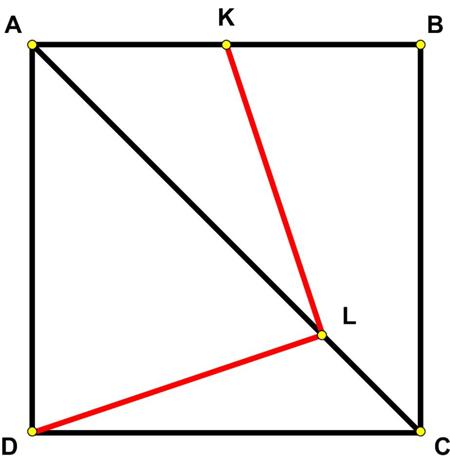 Here is another problem from the “Challenges” section of the Quantum magazine.
Here is another problem from the “Challenges” section of the Quantum magazine. Here is another Quantum math magazine Brainteaser.
Here is another Quantum math magazine Brainteaser. Here is another Brainteaser from the Quantum magazine.
Here is another Brainteaser from the Quantum magazine. Here is another elegant Quantum math magazine Brainteaser problem.
Here is another elegant Quantum math magazine Brainteaser problem. Here is another Brainteaser from the Quantum math magazine.
Here is another Brainteaser from the Quantum math magazine. Here is another elegant Quantum math magazine Brainteaser from the imaginative V. Proizvolov.
Here is another elegant Quantum math magazine Brainteaser from the imaginative V. Proizvolov. Here is another elegant Quantum math magazine Brainteaser problem.
Here is another elegant Quantum math magazine Brainteaser problem.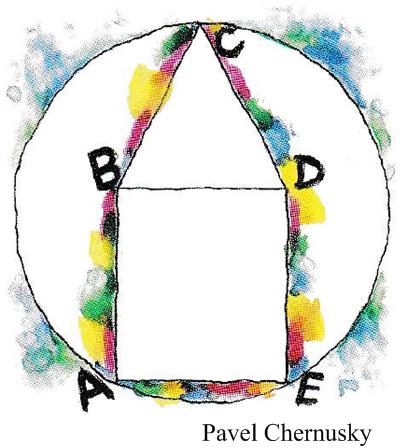 Here is another problem from the “Brainteasers” section of the Quantum magazine.
Here is another problem from the “Brainteasers” section of the Quantum magazine. Here is another Brainteaser from the Quantum magazine.
Here is another Brainteaser from the Quantum magazine.