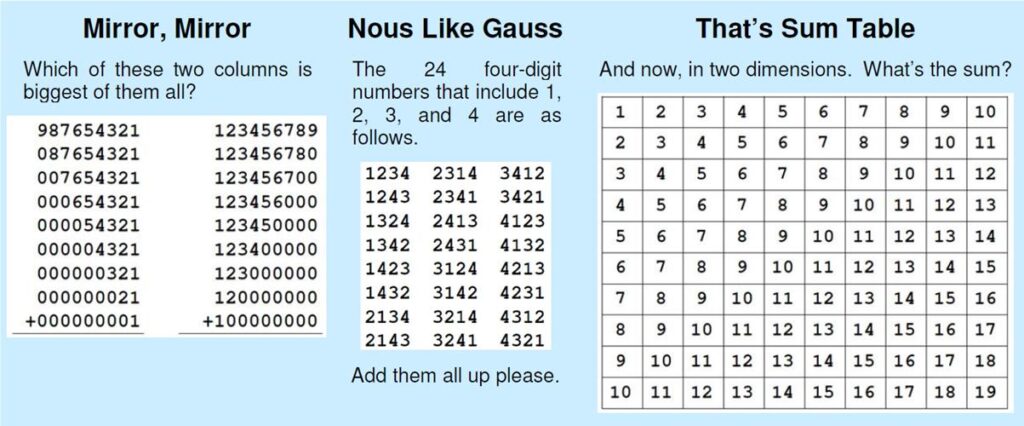
This puzzle from Alex Bellos follows the themes in his new book, The Language Lover’s Puzzle Book, which, among other things, looks at number systems in different languages. (See also his Numberphile video.)
This puzzle from Alex Bellos follows the themes in his new book, The Language Lover’s Puzzle Book, which, among other things, looks at number systems in different languages. (See also his Numberphile video.)
“Today is the International Day of the World’s Indigenous People, which aims to raise awareness of issues concerning indigenous communities. Such as, for example, the survival of their languages. According to the Endangered Languages Project, more than 40 per cent of the world’s 7,000 languages are at risk of extinction.
Among the fantastic diversity of the world’s languages is a diversity in counting systems. The following puzzle concerns the number words of Ngkolmpu, a language spoken by about 100 people in New Guinea. (They live in the border area between the Indonesian province of Papua and the country of Papua New Guinea.)
Ngkolmpu-zzle
Here is a list of the first ten cube numbers (i.e. 13, 23, 33, …, 103):
1, 8, 27, 64, 125, 216, 343, 512, 729, 1000.
Below are the same ten numbers when expressed in Ngkolmpu, but listed in random order. Can you match the correct number to the correct expressions?
eser tarumpao yuow ptae eser traowo eser
eser traowo yuow
naempr
naempr ptae eser traowo eser
naempr tarumpao yuow ptae yuow traowo naempr
naempr traowo yempoka
tarumpao
yempoka tarumpao yempoka ptae naempr traowo yempoka
yuow ptae yempoka traowo tampui
yuow tarumpao yempoka ptae naempr traowo yuow
Here’s a hint: this is an arithmetical puzzle as well as a linguistic one. Ngkolmpu does not have a base ten system like English does. In other words, it doesn’t count in tens, hundreds and thousands. Beyond its different base, however, it behaves very regularly.
This puzzle originally appeared in the 2021 UK Linguistics Olympiad, a national competition for schoolchildren that aims to encourage an interest in languages. It was written by Simi Hellsten, a two-time gold medallist at the International Olympiad of Linguistics, who is currently reading maths at Oxford University.”
See Numbers in New Guinea
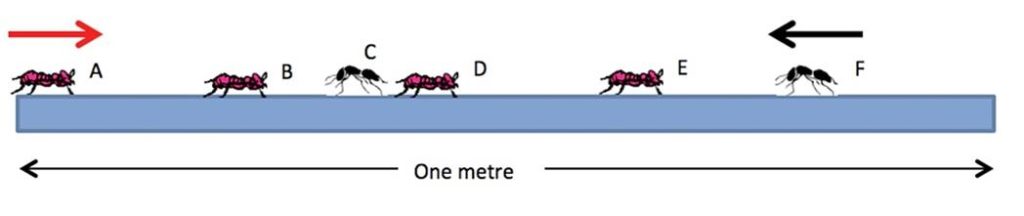
 I think this turned out to be an even trickier problem than Alex Bellos thought.
I think this turned out to be an even trickier problem than Alex Bellos thought.
 This is a recent Alex Bellos
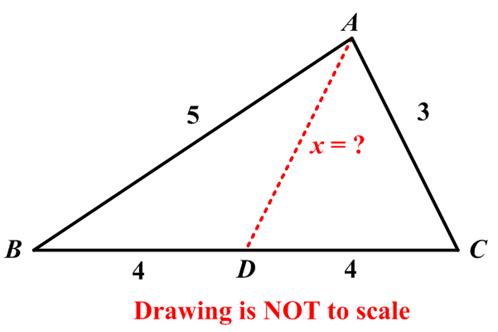
This is a recent Alex Bellos  For his Monday Puzzle in the Guardian Alex Bellos provided a seemingly impossible
For his Monday Puzzle in the Guardian Alex Bellos provided a seemingly impossible 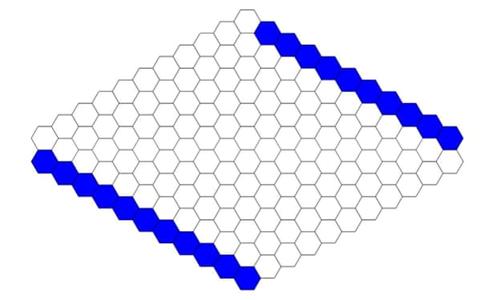
 Unfortunately Ukraine has receded from our attention under the threat from our own anti-democratic forces, but this
Unfortunately Ukraine has receded from our attention under the threat from our own anti-democratic forces, but this 
 This is a fairly straight-forward logic
This is a fairly straight-forward logic  This
This 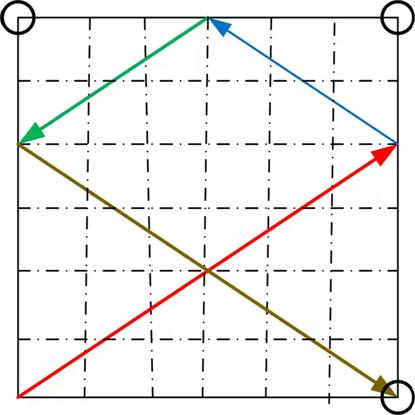 This is a nice
This is a nice  For a change of pace, here is an early
For a change of pace, here is an early