Tag Archives: math history

Horses to Qi

This is a challenging problem from the c.100AD Chinese mathematical work, Jiǔ zhāng suàn shù (The Nine Chapters on the Mathematical Art) found at the MAA Convergence website.

“Now a good horse and an inferior horse set out from Chang’an to Qi. Qi is 3000 li from Chang’an. The good horse travels 193 li on the first day and daily increases by 13 li; the inferior horse travels 97 li on the first day and daily decreases by ½ li. The good horse reaches Qi first and turns back to meet the inferior horse. Tell: how many days until they meet and how far has each traveled?”

The solution involves common fractions, which the Chinese were already adept at using by 100 BC.

Answer.

See Horses to Qi for a solution.

Making Arrows

Alcuin’s Corn Problem

Alcuin of York (735-804) had a series of similar problems involving the distribution of corn among servants. Since the three propositions were the same format with only the numbers changing, I thought I would present them in a more concise form:

“Proposition

A certain head of household had a number of servants, consisting of men, women, and children, among whom he wished to distribute quantities, modia, of corn. The men should receive three modia; the women, two; and the children, half a modium.

(a) If the head of household has 20 servants and wished to distribute 20 modia of corn among them, let him say, he who can, How many men, women and children must there have been.

(b) If the head of household has 30 servants and wished to distribute 30 modia of corn among them, let him say, he who can, How many men, women and children must there have been.

(c) If the head of household has 100 servants and wished to distribute 100 modia of corn among them, let him say, he who can, How many men, women and children must there have been.”

I will give Alcuin’s solutions first, followed by my more expansive solutions that rely on our familiar symbolic algebra that was not available in Alcuin’s time.

See Alcuin’s Corn Problem

A Divine Language

I have just finished reading a most remarkable book by Alec Wilkinson, called A Divine Language: Learning Algebra, Geometry, and Calculus at the Edge of Old Age. I had read an essay of his in the New Yorker that turned out to be essentially excerpts from the book. I was so impressed with his descriptions of mathematics and intrigued by the premise of a mature adult in his 60s revisiting the nightmare of his high school experience with mathematics that I was eager to see if the book was as good as the essay. It was, and more.

The book is difficult to categorize—it is not primarily a history of mathematics, as suggested by Amazon. But it is fascinating on several levels. There is the issue of a mature perspective revisiting a period of one’s youth; the challenges of teaching a novice mathematics, especially a novice who has a strong antagonism for the subject; and insights into why someone would want to learn a subject that can be of no “use” to them in life, especially their later years.

Wilkinson has a strong philosophical urge; he wanted to understand the role of mathematics in human knowledge and the perspective it brought to life. He was constantly asking the big questions: is mathematics discovered or invented, what is the balance between nature and nurture, why does mathematics seem to describe the world so well, what is the link between memorization and understanding, how do you come to understand anything?

See A Divine Language

Symbolic Algebra Timeline

As I am sure is common with most mathematicians, I had become interested in the history of the development of mathematical symbols, first for numbers (numerals) and then for algebra (symbolic algebra). Joseph Mazur’s book Enlightening Symbols provided an excellent history of this evolution. His focus on the development and significance of symbolic algebra in the Renaissance was especially illuminating. I also augmented Mazur’s information with details from Albrecht Heeffer’s work.

Such a subject cries out for a timeline to appreciate the order and timing of discoveries, which Mazur provided, concentrating on the Renaissance. I decided to both simplify Mazur’s version and expand it to cover the evolution of numbers and their notation, as well as to set the whole enterprise in the context of historical periods.

See Symbolic Algebra Timelines

Rotating Plane Problem

Here is another challenging problem from the first issue of the 1874 The Analyst, which also appears in Benjamin Wardhaugh’s book.

“3. If a line make an angle of 40° with a fixed plane, and a plane embracing this line be perpendicular to the fixed plane, how many degrees from its first position must the plane embracing the line revolve in order that it may make an angle of 45° with the fixed plane?

—Communicated by Prof. A. Schuyler, Berea, Ohio.”

Part of the challenge is to construct a diagram of the problem. I used techniques for a solution that were barely in use when this problem was posed in 1874. The contrast between then and now is most revealing.

Answer.

See the Rotating Plane Problem for solutions.

Autumn Sum

Here is another problem from the 2020 Math Calendar.

As a hint, recall that all the answers are integer days of the month. And the solution employs a technique familiar to these pages.

Average.

See Autumn Sum for a solution.

The Triangle of Abū’l-Wafā’

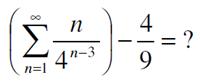
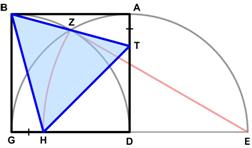I found an interesting geometric statement in a paper of Glen Van Brummelen cited in the online MAA January 2020 issue of Convergence:

“For instance, Abū’l-Wafā’ describes how to embed an equilateral triangle in a square, as follows: extend the base GD by an equal distance to E. Draw a quarter circle with centre G and radius GB; draw a half circle with centre D and radius DE. The two arcs cross at Z. Then draw an arc with centre E and radius EZ downward, to H. If you draw AT = GH and connect B, H, and T, you will have formed the equilateral triangle.”

So the challenge is to prove this statement regarding yet another fascinating appearance of an equilateral triangle.

See the Triangle of Abū’l-Wafā’

The Za’irajah and Mathematics

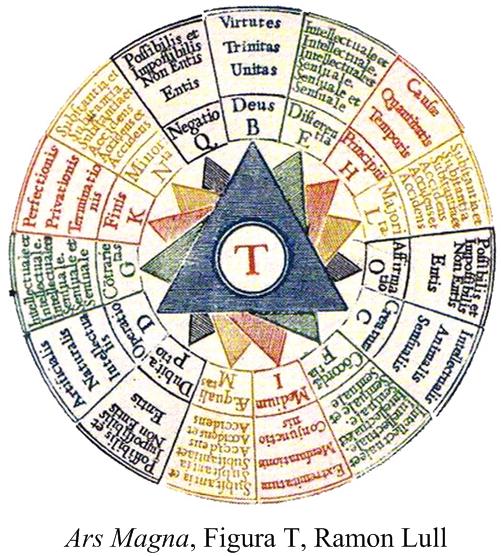The subtext of this essay might be “word problems,” since the stream of thoughts that led to the za’irajah (zairja) began with a paper I read, while searching for potential problems for this website, on the history of word problems in high school texts in algebra in the 20th and 21st centuries. The following statement by Lorenat caught my attention:

“The newer characteristics of how word problems are treated in Long’s text [2016] … include adding sympathetic commentary about fear of word problems. ‘And of course, there are those dreaded “Word Problems,” but I’ve solved them all for you, so they’re painless.’

[Lorenat continues,] A more extreme example of this is exhibited in the word problem commentary of Michael W. Kelley’s The Idiot’s Complete Guide to Algebra: Second Edition from 2007, in which he describes word problems as ‘a necessary evil of algebra, jammed in there to show you that you can use algebra in “real life.”’ However, Kelley makes no attempt to write ‘real life’ word problems, and criticizes the uselessness of the word problems he does include.”

This essay is an attempt to rebut such negative views of solving word problems by placing the activity in a more favorable historical context.

See the Za’irajah and Mathematics

Fibonacci, Chickens, and Proportions

There is the famous chicken and the egg problem: If a chicken and a half can lay an egg and a half in a day and a half, how many eggs can three chickens lay in three days? Fibonacci 800 years ago in his book Liber Abaci (1202 AD) did not have exactly this problem (as far as I could find), but he posed its equivalent. And most likely the problem came even earlier from the Arabs. So we can essentially claim Fibonacci (or the Arabs) as the father of the chicken and egg problem. Here are three of Fibonacci’s actual problems:

“Five horses eat 6 sestari of barley in 9 days; it is sought by the same rule how many days will it take ten horses to eat 16 sestari.
A certain king sent indeed 30 men to plant trees in a certain plantation where they planted 1000 trees in 9 days, and it is sought how many days it will take for 36 men to plant 4400 trees.
Five men eat 4 modia of corn in one month, namely in 30 days. Whence another 7 men seek to know by the same rule how many modia will suffice for the same 30 days.”

By modern standards these problems all involve simple arithmetic to solve. But there are actually some subtleties in mapping the mathematical model to the situation, in which fractions, proportions, ratios, and “direct variation” get swirled into the mix—naturally causing some confusion.

Answers.

See Fibonacci, Chickens, and Proportions for a solution.

Meditations on Mathematics

A compendium of puzzles, problems, math inquiries, and math commentary.