 This problem is from Colin Hughes’s Maths Challenge website (mathschallenge.net).
This problem is from Colin Hughes’s Maths Challenge website (mathschallenge.net).
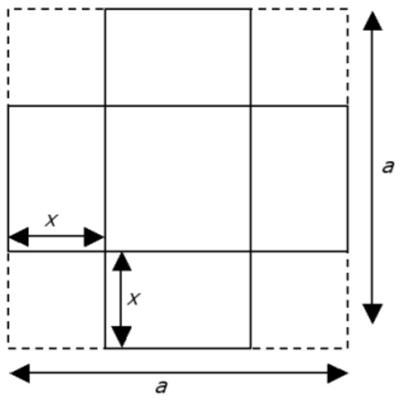
“Four corners measuring x by x are removed from a sheet of material that measures a by a to make a square based open-top box. Prove that the volume of the box is maximised iff the area of the base is equal to the area of the four sides.”
See the Maximized Box Problem

The Maximized Box Problem can be proved using just algebra, no calculus is required in my approach.
Proof plan:
1- Determine the conditions when base area equals four sides area.
2. Evaluate volumen under that condition.
3. Prove that the volume is smaller under any other conditions.
Proof:
1. Define b:square base side; h=altitude of box.
Area of the base=b^2; Area of each lateral=b*h.
It is required that b^2=4b*h or b=4h.
But 2h+b=a, then 2h+4h=a or 6h=a.
Then conditions are h=a/6, b=4a/6
2. To simplify let’s say h=1, b=4, a=6.
Then volumen under required conditions is 16.
3. Other conditions means h=1+Δ, b=4-2Δ
with Δ not zero and -1<Δ<2.
Volume is V=(4-2Δ)²(1+Δ)=16-12Δ²+4Δ³
That may be rewritten as V=16+[4Δ²(Δ-3)]
Since Δ<2 the expression into [ ] is negative
Then V<16 if Δ not zero.
Q.E.D.