This is a straight-forward problem from the Scottish Mathematical Council (SMC) Senior Mathematics Challenge.
“A circle has radius 1 cm and AB is a diameter. Two circular arcs of equal radius are drawn with centres A and B. These arcs meet on the circle as shown. Calculate the shaded area.”
There are several possible approaches and the SMC offers two examples.
See the Moon Quarters Problem for solution.
This puzzle from the Scottish Mathematical Council (SMC) Senior Mathematics Challenge seems at first to have insufficient information to solve.
“Ant and Dec had a race up a hill and back down by the same route. It was 3 miles from the start to the top of the hill. Ant got there first but was so exhausted that he had to rest for 15 minutes. While he was resting, Dec arrived and went straight back down again. Ant eventually passed Dec on the way down just half a mile before the finish.
Both ran at a steady speed uphill and downhill and, for both of them, their downhill speed was one and a half times faster than their uphill speed. Ant had bet Dec that he would beat him by at least a minute.
Did Ant win his bet?”
See the Close Race Puzzle for solutions.
(Update 1/2/2023) Alternative Solution from Oscar Rojas Continue reading
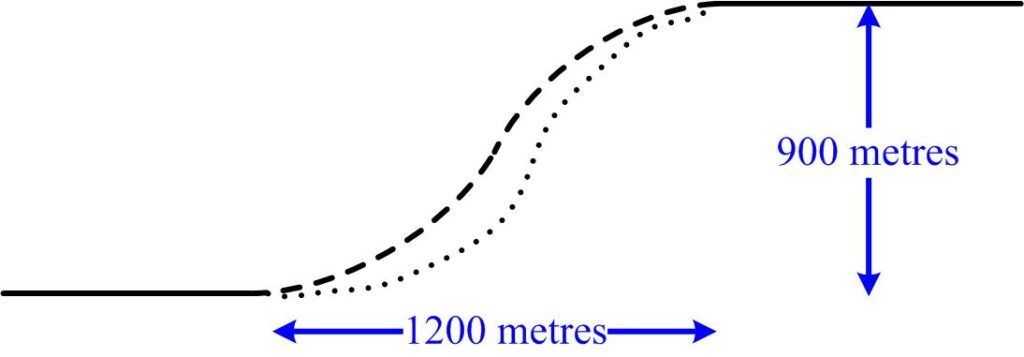This is an interesting problem from the Scottish Mathematics Council (SMC) 2014 Senior Math Challenge .
“Two straight sections of a road, each running from east to west, and located as shown, are to be joined smoothly by a new roadway consisting of arcs of two circles of equal radius. The existing roads are to be tangents at the joins and the arcs themselves are to have a common tangent where they meet. Find the length of the radius of these arcs.”
See the Road Construction Problem for solutions.
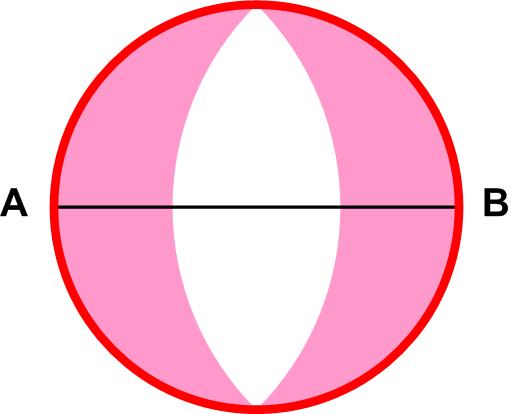
This puzzle from the Scottish Mathematical Council (SMC) Middle Mathematics Challenge has an interesting twist to it.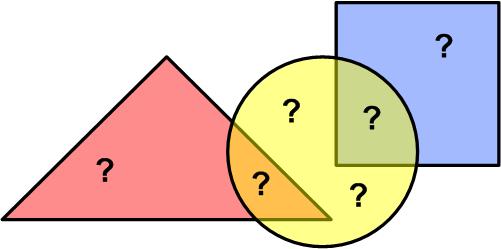
“Two young mountaineers were descending a mountain quickly at 6 miles per hour. They had left the hostel late in the day, had climbed to the top of the mountain and were returning by the same route. One said to the other “It was three o’clock when we left the hostel. I am not sure if we will be back before nine o’clock.” His companion replied “Our pace on the level was 4 miles per hour and we climbed at 3 miles per hour. We will just make it.” What is the total distance they would cover from leaving the hostel to getting back there?”
See the Mountain Climbing Puzzle for solutions.
This is a nice puzzle from the Scottish Mathematical Council (SMC) Senior Mathematical Challenge of 2008. It is more a logic puzzle than a geometric one.
“In the diagram, each question mark represents one of six consecutive whole numbers. The sum of the numbers in the triangle is 39, the sum of those in the square is 46 and the sum of those in the circle is 85. What are the six numbers?”
See the Shared Spaces Puzzle
This problem comes from the Scottish Mathematical Council (SMC) Senior Mathematical Challenge of 2007:
“A group of seven girls—Ally, Bev, Chi-chi, Des, Evie, Fi and Grunt—were playing a game in which the counters were beans. Whenever a girl lost a game, from her pile of beans she had to give each of the other girls as many beans as they already had. They had been playing for some time and they all had different numbers of beans. They then had a run of seven games in which each girl lost a game in turn, in the order given above. At the end of this sequence of games, amazingly, they all had the same number of beans—128. How many did each of them have at the start of this sequence of seven games?”
See the Seven Girls Puzzle for solutions.
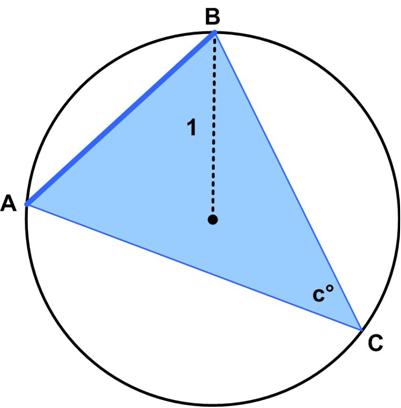This is another nice puzzle from the Scottish Mathematical Council (SMC) Senior Mathematical Challenge of 2008.
“The triangle ABC is inscribed in a circle of radius 1. Show that the length of the side AB is given by 2 sin c°, where c° is the size of the interior angle of the triangle at C.”
The diagram shows the case where C is on the same side of the chord AB as the center of the circle. There is a second case to consider where C is on the other side of the chord from the center.
See the Circle Chord Problem
This is a nice geometric problem from the Scottish Mathematical Council (SMC) Senior Mathematical Challenge of 2008.
“Mahti has cut some regular pentagons out of card and is joining them together in a ring. How many pentagons will there be when the ring is complete?
She then decides to join the pentagons with squares which have the same edge length and wants to make a ring as before. Is it possible? If so, determine how many pentagons and squares make up the ring and if not, explain why.”
See the Polygon Rings for solutions.
This problem comes from the Scottish Mathematical Council (SMC) Senior Mathematical Challenge of 2008:
“S2. In Tiffany’s, a world famous jewellery store, there is a string necklace of 33 pearls. The middle one is the largest and most valuable. The pearls are arranged so that starting from one end, each pearl is worth $100 more than the preceding one, up to [and including] the middle one; and starting from the other end, each pearl is worth $150 more than the preceding one, up to [and including] the middle one. If the total value of the necklace is $65,000 what is the value of the largest pearl?”
I included the words in brackets to erase any ambiguity.
See the Pearl Necklace Problem for solutions.
