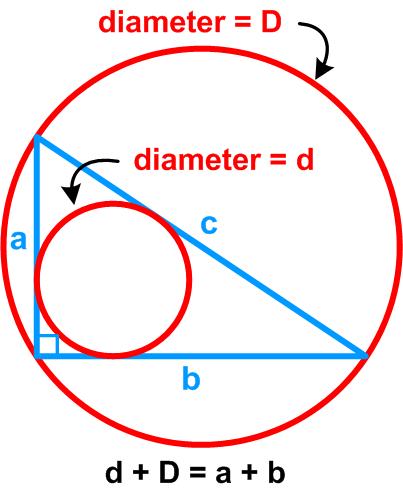
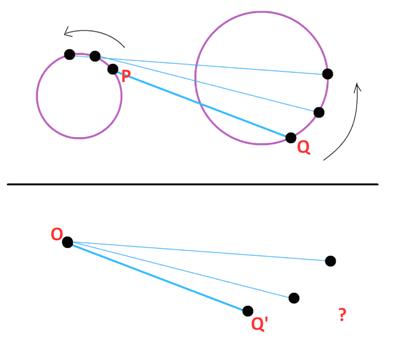
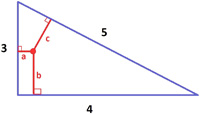
James Tanton asked to prove the following surprising property of a right triangle and its circumscribed and inscribed circles.
“Every triangle is circumscribed by some circle of diameter D, say, and circumscribes another circle of smaller diameter d. For a right triangle, d + D equals the sum of two side lengths of the triangle. Why?”
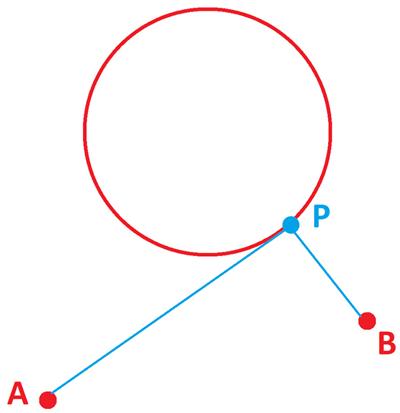James Tanton provides another imaginative problem on Twitter.
“I am at point A and want to walk to point B via some point, any point, P on the circle. What point P should I choose so that my journey A → P → B is as short as possible?”
Hint: I got ideas for a solution from two of my posts, “Square Root Minimum” and “Maximum Product”.
Here is a seemingly simple problem from Futility Closet.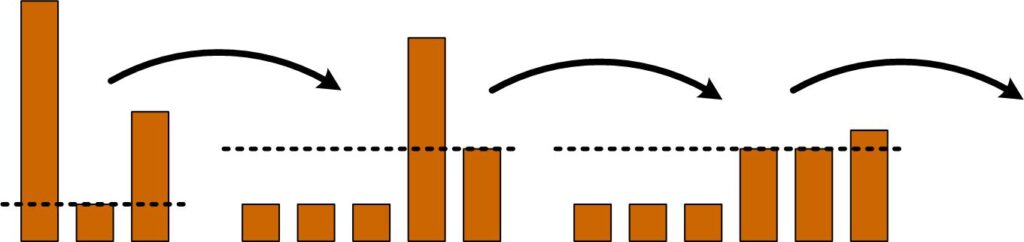
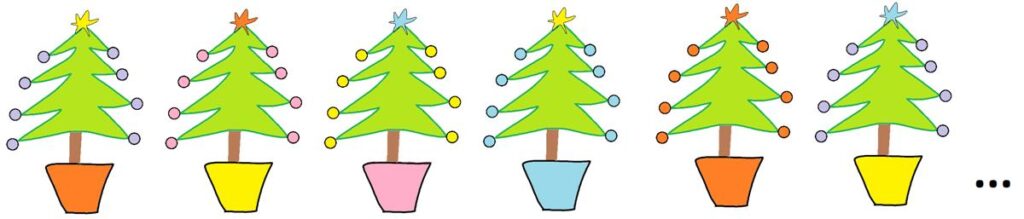
“A quickie from Peter Winkler’s Mathematical Puzzles, 2021: Can West Virginia be inscribed in a square? That is, is it possible to draw some square each of whose four sides is tangent to this shape?”
Technically we might rephrase this as, can we inscribe a flat map of West Virginia in a square, since the boundary of most states is probably not differentiable everywhere, that is, has a tangent everywhere.
But the real significance of the problem is that it is an example of an “existence proof”, which in mathematics refers to a proof that asserts the existence of a solution to a problem, but does not (or cannot) produce the solution itself. These proofs are second in delight only to the “impossible proofs” which prove that something is impossible, such as trisecting an angle solely with ruler and compass.
Here is another classic example (whose origin I don’t recall). Consider the temperatures of the earth around the equator. At any given instant of time there must be at least two antipodal points that have the same temperature. (Antipodal points are the opposite ends of a diameter through the center of the earth.)
See Existence Proofs (revised)
(Update 10/2/2021) I fixed a minor typo: “tail” should have been “head”
This is another thoughtful puzzle from the imaginative mind of James Tanton (with slight edits).
“Three poles of height 1183 feet, 182 feet, 637 feet stand in the ground. Pick a pole and saw off all the taller poles at that height. Plant those tops in the ground too. Repeat until no more such saw cuts can be made. Despite choices made along the way, what final result is sure to occur? [Four poles, heights a, b, c, d ft?]”
See the Pole Leveling Puzzle for a solution.
James Tanton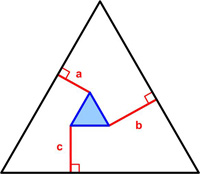 has come up with another imaginative concrete problem harboring a mathematical pattern.
“60 trees in a row. Their stars are yellow, orange, blue, Y, O, B, Y, O, B, … Their pots are orange, yellow, pink, blue, O, Y, P, B, O, Y, P, B, … Their baubles are mauve, pink, yellow, blue, orange, M, P, Y, B, O, M, P, Y, B, O, … Must there be an all yellow tree? All B? One with star = O, pot = O, baubles = M?”
See the Christmas Tree Puzzle for a solution.
This is a stimulating little problem from the ever-creative James Tanton:
“An ant is at the east end of an infinite stretchy band, initially 2 ft long. Each day: ant walks 1 ft west on the band. Overnight while sleeping, band stretches to double its length (carrying ant westward as does so). Same routine each day/night. Will ant cover 99% of band’s length?”
(Ant from clipart-library.com)
See the Rubber Band Ant for solutions.
James Tanton had another interesting puzzle on Twitter.
“Points P and Q each move counterclockwise on a circle, uniform speed, one revolution per minute. At each instant, segment PQ is translated so that P is at the origin. Let Q’ be the image of Q. What curve is traced by the points Q’?”
See the Tandem Circles for an answer.
James Tanton has provided further elaborations on the polygons and the sum of perpendicular distances from interior points. Again I approached the solutions with a mix of areas and vectors. It is rather impressive to see the number of variations that can be rung on the Viviani Theorem theme. See Polygon Altitude Problems II
I found this collection of related problems by James Tanton on Twitter. Even though all these problems do not involve perpendiculars, they have a common solution approach – a sort of theme and variations idea. In a later tweet Tanton refers to a Viviani Theorem associated with these types of problems. I did not recall that theorem explicitly or by name. I also have not looked it up yet, in order to solve these problems on my own. I am guessing there is a more classical Euclidean geometry proof, but I like my vector approach for its clarity. I also throw in a bit a calculus at the end for fun. See Polygon Altitude Problems I
