 This is an intriguing puzzle from Futility Closet.
This is an intriguing puzzle from Futility Closet.
“In Robert Chambers’ 1906 novel The Tracer of Lost Persons, Mr. Keen copies the figure below from a mysterious photograph. He is trying to help Captain Harren find a young woman with whom he has become obsessed.
‘It’s the strangest cipher I ever encountered,’ he says at length. ‘The strangest I ever heard of. I have seen hundreds of ciphers—hundreds—secret codes of the State Department, secret military codes, elaborate Oriental ciphers, symbols used in commercial transactions, symbols used by criminals and every species of malefactor. And every one of them can be solved with time and patience and a little knowledge of the subject. But this … this is too simple.’
The message reveals the name of the young woman whom Captain Harren has been seeking. What is it?”
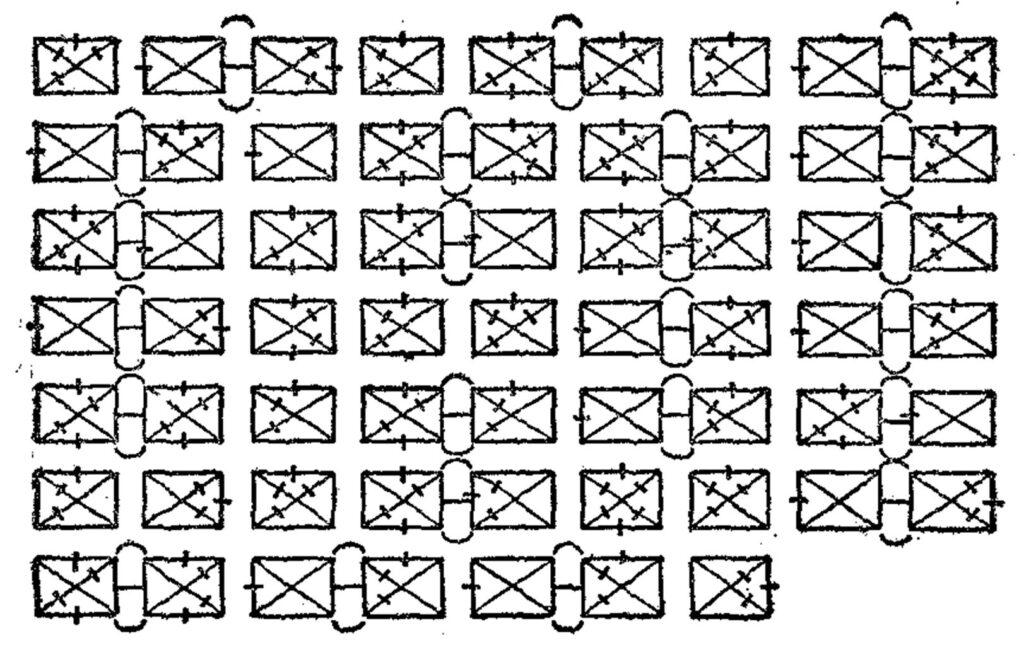
As is usual with these types of puzzles, I felt foolish that I couldn’t see the immediate, simple interpretation of the boxes—after a great deal of effort. So I solved it using the usual cryptographic methods that rely heavily on logic and letter frequencies, though the message is a bit short for that.
See Box Code Puzzle for solutions.

 One is reduced to hysterical laughter to try to maintain a modicum of sanity.
One is reduced to hysterical laughter to try to maintain a modicum of sanity.
 The June 2023
The June 2023  For his Monday Puzzle in the Guardian Alex Bellos provided a seemingly impossible
For his Monday Puzzle in the Guardian Alex Bellos provided a seemingly impossible 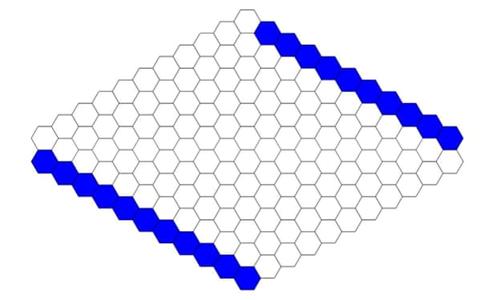
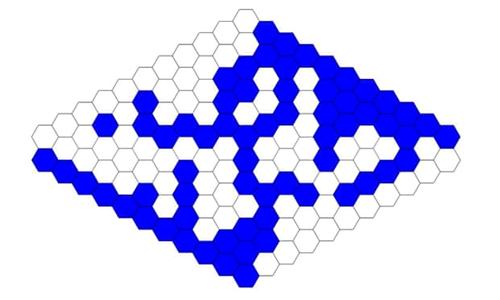
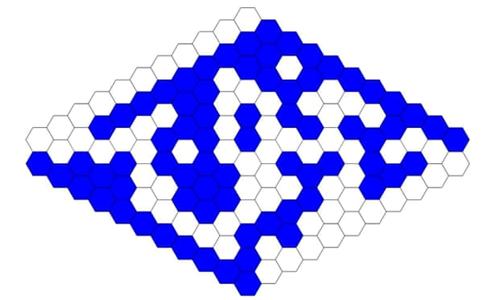


 This is a fun logic
This is a fun logic  Unfortunately Ukraine has receded from our attention under the threat from our own anti-democratic forces, but this
Unfortunately Ukraine has receded from our attention under the threat from our own anti-democratic forces, but this 
 This
This 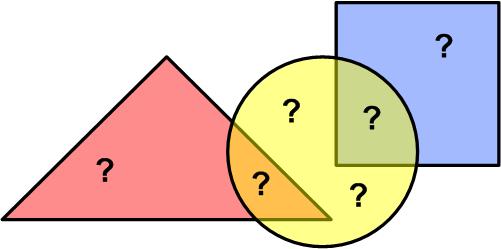 This is a nice puzzle from the Scottish Mathematical Council (SMC) Senior Mathematical Challenge of 2008. It is more a logic puzzle than a geometric one.
This is a nice puzzle from the Scottish Mathematical Council (SMC) Senior Mathematical Challenge of 2008. It is more a logic puzzle than a geometric one. This is a fairly straight-forward logic
This is a fairly straight-forward logic