Category Archives: Other Voices

Survival of Records

I have written about this a bit in my “Symbolic Algebra Timelines” post as part of the discussion of how Greek mathematics got transmitted to the present.

I had read an article by the renowned literary historian Gilbert Highet some sixty years ago which I never forgot.  It discussed in some detail the miracle of the survival of records from the past.  I tried to find a copy online, but in vain.  So I purchased a used 1962 copy of the now extinct Horizons that contained the article and proceeded to digitize it.  Since the subject of the article is about disappearing writings of the past and how some managed to survive through reproduction, I feel it somewhat apropos that I allow it to see the light of day again.  He is a marvelous writer and covers the subject with fascinating detail.

Even with all the losses Highet records, writings still survived because they were in some sort of hard copy form. By 1962 fragile documents such as newspapers were being moved to microfilm.  But microfilm was often replaced by magnetic tape, which was in turn replaced by a succession of digital media: floppy discs, CDs, DVDs, memory sticks, and so on. Finally, local media is being replaced by files in the “cloud”. All these media are subject to deterioration and loss, or the whims of the custodians. And of course, they all need machines and software to retrieve their information—technology which may no longer exist. Terabytes of moon data are lost on Ampex magnetic tapes for which there are no analog tape readers or even records of the data formats. Even now, some books are being published electronically and not in hard copy.  Some people have referred to this ephemeral situation as the “digital Dark Age” where everything can be lost—often in an instant.  So perhaps we are lucky that records from the past were not digital.

My copy of Highet’s article appears in two forms: a full, but very large, version with all the color figures, Survival of Records (58 MB), and a text-only smaller version, Survival of Records wo figs (700 KB).

Counting Tanks

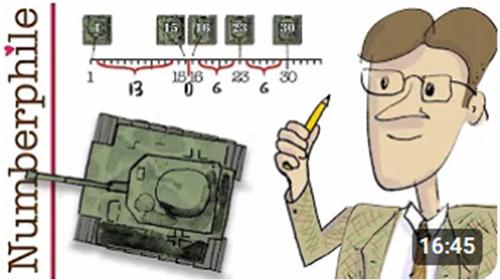A great example of the application of simple math to real-world problems is provided in a recent Numberphile video on YouTube by the British mathematician James Grime.

It is taken from a real story from World War II where the British were trying to estimate the number of tanks the Germans were producing each month.  The spies came up with an estimate of about 1500 tanks per month, whereas the mathematicians estimated the number to be closer to 250 tanks per month.  How the mathematicians did this is explained by Grime.  (I added an explanation of one step that whizzed by in Grime’s presentation and that I didn’t understand at first.)

See Counting Tanks.

Aunt Hillary and the Anteater

In this moment when the collective actions of humans seem to be hurtling towards several cataclysms (burning up the planet, ending the American Experiment), I am reminded of a powerful image that invaded my psyche some 45 years ago.  It was from Douglas Hofstadter’s magnum opus, Gödel, Escher, Bach (1979) and concerned his investigation of what became popularized as “emergent behavior” and “self-organization.”  This was in the early days of chaos theory and Holland’s emerging complexity theory.  Conway’s artificial life cellular automaton, the Game of Life, was the screen saver on countless computer terminals and burgeoning personal computers.  It was also the time when neural nets were beginning to capture the imagination of machine learning researchers among the artificial intelligence community.

Hofstadter’s aim was to explore these ideas as they related to understanding the brain and he used the vehicle of an ant colony.

See Aunt Hillary and the Anteater.

Also see the excerpt Ant Fugue (2.5 MB) and the Atlantic article “What the Microsoft Outage Reveals”.

Danica McKellar Interview

I recently watched a remarkable and surprising interview on Numberphile of the actress Danica McKellar.  She began as a child actress and recently has played romantic roles on the Hallmark series of TV movies.  So it comes as a surprise to find she was an undergraduate math major, and with a female colleague and the help of their advisor one summer proved a theorem involving math and metallurgy.

She was terrifically articulate and enthusiastic during the interview and made a number of telling observations that would be helpful for any student, especially girls, who might find they like math in grade school and might even consider majoring in it in college.

Her big emphasis was on self-esteem and the importance of reaching girls to support any interest they might have in math against the negative forces they often experience.  To this end she has written a series of math books, each tailored to a different grade-level of students.  But she feels the middle school years are especially critical to support girls in math.

Perhaps the thing I liked best in the interview (maybe because it echoed my own views) was her attitude towards math—she loved solving puzzles.  In fact, just doing math was its own reward.  She politely deflected all efforts by Brady, the interviewer, to ask if she regretted not pursuing a professional career more devoted to math.  Not to knock Brady’s fine interview but I found this line of questioning supporting the current utilitarian view of education (What good is it, how can it be of use to help me earn a living) to be a bit condescending.  And there was even a whiff of what the most important thing to do with math and what the professors are training students for is math research.   Since most math majors and even math Ph.D.s are not going to find employment in academia, math as an ancillary component to one’s career is the most one could imagine in this context.  But above and beyond that is the real truth: math is fun for its own sake, and Danica McKellar championed that in spades.  I don’t think I have seen anyone unabashedly extol the joys of doing math as well as she did.

I heartily recommend this interview to anyone, especially young girls, who might have a secret affection for mathematics but fear some stigma that might attach to them if they admitted it.

Some links from Youtube:

For a PDF version see Danica McKellar Interview.

A New Day

One of the physics blogs I enjoy reading is by the mathematical physicist Peter Woit, called Not Even Wrong.  A recent post provided a tantalizing teaser:

“I want to [link to] an insightful explanation of the history of string theory, discussing the implications of how it was sold to the public. It’s by a wonderful young physicist I had never heard of before, Angela Collier. She has a Youtube channel, and her latest video is string theory lied to us and now science communication is hard.

… It’s as hilarious as it is brilliant, and you have to see for yourself.”

Collier delivered her talk lucidly and thoroughly—all while playing a frenetic video game!  She claimed she used the length of the game to time her talk.  Of course we can walk and talk, and ride bicycles and talk, but I have never seen anyone split their mental concentration between a fast-paced video game and an esoteric physics explanation of the history of string theory and supersymmetry—for over 50 minutes!  And there was something about her presentation that was completely captivating.  It was definitely a serious scientific talk, but the ludicrousness of the game-playing echoed how ridiculous the continued, misplaced fascination with string theory is.  Naturally I had to learn more about this provocative physicist.

See A New Day

A Divine Language

I have just finished reading a most remarkable book by Alec Wilkinson, called A Divine Language: Learning Algebra, Geometry, and Calculus at the Edge of Old Age.  I had read an essay of his in the New Yorker that turned out to be essentially excerpts from the book.  I was so impressed with his descriptions of mathematics and intrigued by the premise of a mature adult in his 60s revisiting the nightmare of his high school experience with mathematics that I was eager to see if the book was as good as the essay.  It was, and more.

The book is difficult to categorize—it is not primarily a history of mathematics, as suggested by Amazon. But it is fascinating on several levels.  There is the issue of a mature perspective revisiting a period of one’s youth; the challenges of teaching a novice mathematics, especially a novice who has a strong antagonism for the subject; and insights into why someone would want to learn a subject that can be of no “use” to them in life, especially their later years.

Wilkinson has a strong philosophical urge; he wanted to understand the role of mathematics in human knowledge and the perspective it brought to life.  He was constantly asking the big questions:  is mathematics discovered or invented, what is the balance between nature and nurture, why does mathematics seem to describe the world so well,  what is the link between memorization and understanding, how do you come to understand anything?

See A Divine Language

Abraham Lincoln, Technologist

I thought there was nothing new we could learn about Abraham Lincoln, but I see I was quite mistaken after reading Sidney Blumenthal’s article,  “Abraham Lincoln, Tech Entrepreneur”.

In the current oppressive anti-science climate it is important to look back at our history and see how integral scientific thinking was to our founding and development.  Not only were our Founding Fathers scientists, such as Jefferson and Franklin who with others founded the American Philosophical Society in 1743, but it turns out that President Abraham Lincoln could also lay claim to a scientific mind.  Blumenthal’s article describes in detail how Lincoln employed science to advance the development of our country.  You should read the entire article, but I am including some highlights.

See Abraham Lincoln Technologist

The Bourbaki World

I thought it would be interesting to present a recent entry in the mathematician John Baez’s Diary on some extremes in mathematics from the Bourbaki school, namely, how many symbols it would take to define the number “1.”

I don’t know if the “mathematician” Nicolas Bourbaki holds any significance for students today, but in my time (math graduate school in the 1960s) the Bourbaki approach seemed to permeate everything.

My first exposure to Bourbaki was as a humorous figure described by Paul Halmos in his 1957 article in the Scientific American—the humor being that Bourbaki did not exist.  As Halmos wrote:

“One of the legends surrounding the name is that about 25 or 30 years ago first-year students at the Ecole Normale Superieure (where most French mathe­maticians get their training) were annually exposed to a lecture by a dis­tinguished visitor named Nicolas Bour­baki, who was in fact an amateur actor disguised in a patriarchal beard, and whose lecture was a masterful piece of mathematical double-talk.  It is necessary to insert a word of warning about the unreliability of most Bourbaki stories. While the members of this cryptic organization have taken no blood oath of secrecy, most of them are so amused by their own joke that their stories about themselves are intentionally conflicting and apocryphal.”

Nicholas Bourbaki was the pseudonym for a group of French mathematicians who wished to write a treatise which would be, as Halmos stated, “a survey of all mathematics from a sophisticated point of view”.

See the Bourbaki World

Coronavirus Mathematics

Given the mathematical nature of this website I feel reluctantly impelled to address the coronavirus pandemic. The mathematics behind the spread of infection is basically the same exponential growth that I discussed in the “Math and Religion” post and has recently been explained by the ever-lucid Grant Sanderson at his 3Blue1Brown website.

What I wish to draw attention to is the series of posts on the coronavirus by Kevin Drum on his website at Mother Jones. I have collected his recent posts comparing the spread of the virus in various countries and added some mathematical commentary of my own, which is the content of this post.

But the bottom line seems to be that in virtually all the countries, including the US, the virus infection is spreading at the Italian rate of doubling every 4 days! The readers of this website are sufficiently numerate to realize the frightening import of that number. If that weren’t enough, Kevin provides additional posts on the results of the modeling at the Imperial College that are truly nerve-wracking for someone such as myself in the most vulnerable cohort. The only blessing so far seems to be that, for once, the children are spared.

At this time, I don’t have the stomach to keep updating the post as new numbers come in. That may change. I could address the catastrophe of having ignorance and incompetence at the helm of the national ship of state, but it is too depressing.

See the Coronavirus Mathematics

(Updates 3/17/2020, 3/21/2020, 4/17/2020, 9/20/2020, 10/1/2020)  Continue reading →

  1. Pages:
  2. 1
  3. 2