Here is another classic example of the three jug problem posed in the Mathigon Puzzle Calendars for 2017.
“How can I measure exactly 8 liters of water, using just one 11 liter and one 6 liter bucket?”
It is assumed you have unlimited access to water (the “third jug” of at least 17 liters). You can only fill or empty the jugs, unless in poring from one jug to another you fill the receiving jug before emptying the poring jug. (Hint: see the Three Jugs Problem.)
See Two More Jugs.
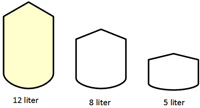I was sifting back through some problems posed by Presh Talwalkar on his website Mind Your Decisions, when I found another 3 Jugs problem, which was amenable to the skew billiard table solution from my earlier Three Jugs Problem. Here is his statement:
“A milkman carries a full 12-liter container. He needs to deliver exactly 6 liters to a customer who only has 8-liter and a 5-liter containers. How can he do this? No milk should be wasted: the milkman needs to leave with 6 liters of milk. Can he measure all amounts of milk from 1 to 12 (whole numbers) in some container?”
I also believe I found a case where Talwalkar’s solution to the last question needs revision. See the Three Jugs Problem Redux for solutions.
This is another problem from the defunct Wall Street Journal Varsity Math Week column.
“Team member Janice recently visited the U.K. and poses this puzzle to her teammates: You have three containers that can hold exactly 15, 10 and 6 pints. The 15-pint container starts full of cider. You want to measure out exactly 2 pints of cider, drink it all, and end with an empty 15-pint container and 8 and 5 pints of cider in the other two containers. What transfers should you make to accomplish this?”
The solution is based on my Three Jugs Problem. See Two Pints of Cider.
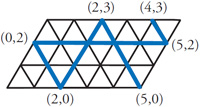Years ago (1967) I read about an interesting solution to the three jugs problem in a book by Nathan Court which involved the idea of a billiard ball traversing a skew billiard table with distributions of the water between the jugs listed along the edges of the table. The ball bounced between solutions until it ended on the desired value. I thought it was very clever, but I really did not understand why it worked. Later I figured out an explanation, which I present here. See the Three Jugs Problem.
