This problem from Colin Hughes at Maths Challenge is a most surprising result that takes a bit of tinkering to solve.

“Problem
We can see that 3 x 4 x 5 x 6 = 360 = 19² – 1. Prove that the product of four consecutive integers is always one less than a perfect square.”

The result is so mysterious at first that you begin to understand why the ancient Pythagoreans had a mystical relationship with mathematics.

See the Consecutive Product Square.

(Update 11/12/2020) Generalization and Visual Proof

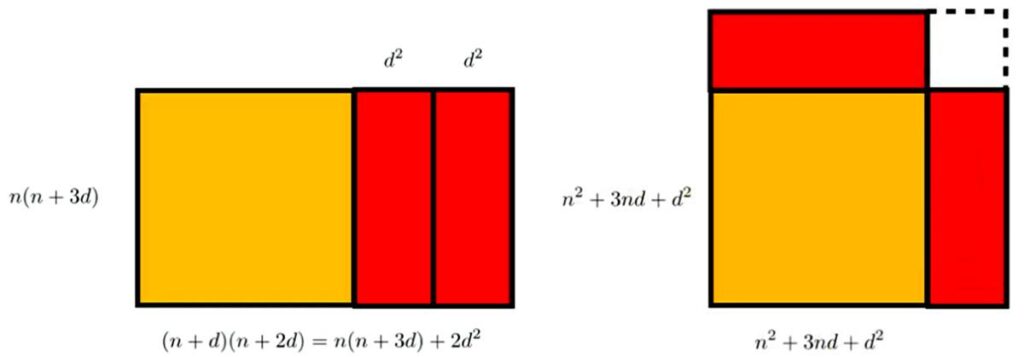
From Fermat’s Library on 4 November 2020 we have a visual proof of a generalization of the consecutive integer problem:

“A visual proof that the product of 4 positive integers in arithmetic progression is the difference of two squares

n(n + d)(n + 2d)(n + 3d) = (n² + 3nd + d²)² – (d²)² ”