This is a fun problem from the 1949 Eureka magazine.
“The following problems were set at the Archimedeans’ 1949 Problems Drive. Competitors were allowed five minutes for each question. [This is problem #9.]
A pillar is in the form of a truncated right circular cone. The diameter at the top is 1 ft., at the bottom it is 2 ft. The slant height is 15 ft. A streamer is wound exactly five times round the pillar starting at the top and ending at the bottom. What is the shortest length the streamer can have?”
See the Pillar Wrapping Problem
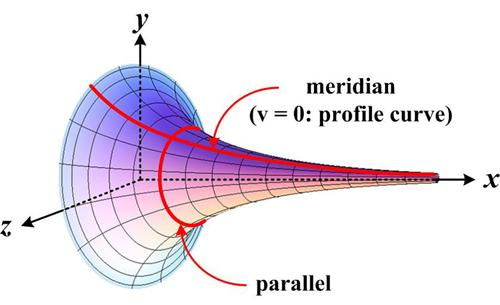This essay began as an effort to prove Tanya Khovanova’s statement in her article “The Annoyance of Hyperbolic Surfaces” that her crocheted hyperbolic surface had constant (negative) curvature. I discussed Khovanova’s article in my previous essay “
When our daughter-in-law made wheat shocks as center-pieces for hers and our son’s fall-themed wedding reception, I naturally could not help pointing out the age-old observation that they represented a hyperboloid of one sheet. This was naturally greeted with the usual groans, but the thought stayed with me as I realized I had never proved this mathematically to myself. And so I did.