 This 2007 four-star problem from Colin Hughes at Maths Challenge is definitely a bit challenging.
This 2007 four-star problem from Colin Hughes at Maths Challenge is definitely a bit challenging.
“Problem
For any positive integer, k, let Sk = {x1, x2, … , xn} be the set of [non-negative] real numbers for which x1 + x2 + … + xn = k and P = x1 x2 … xn is maximised. For example, when k = 10, the set {2, 3, 5} would give P = 30 and the set {2.2, 2.4, 2.5, 2.9} would give P = 38.25. In fact, S10 = {2.5, 2.5, 2.5, 2.5}, for which P = 39.0625.
Prove that P is maximised when all the elements of S are equal in value and rational.”
I took a different approach from Maths Challenge, but for me, it did not rely on remembering a somewhat obscure formula. (I don’t remember formulas well at my age—only procedures, processes, or proofs, which is ironic, since at a younger age it was just the opposite.) It is also clear from the Maths Challenge solution that the numbers were assumed to be non-negative.
See Maximum Product.
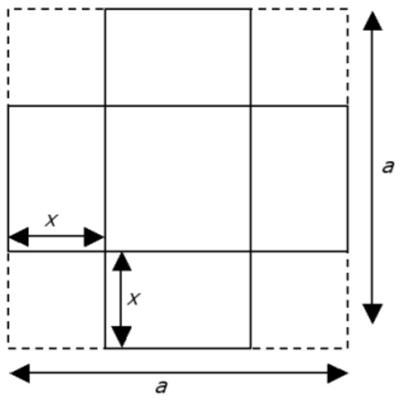 This problem is from Colin Hughes’s Maths Challenge website (mathschallenge.net).
This problem is from Colin Hughes’s Maths Challenge website (mathschallenge.net).
 This is another physics-based problem from Colin Hughes’s Maths Challenge website (mathschallenge.net) that may take a bit more thought.
This is another physics-based problem from Colin Hughes’s Maths Challenge website (mathschallenge.net) that may take a bit more thought. This math problem from Colin Hughes’s Maths Challenge website (mathschallenge.net) hearkens back to basic physics.
This math problem from Colin Hughes’s Maths Challenge website (mathschallenge.net) hearkens back to basic physics.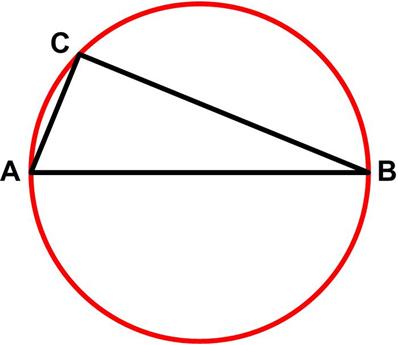 This math problem from Colin Hughes’s Maths Challenge website (mathschallenge.net) is a bit more challenging.
This math problem from Colin Hughes’s Maths Challenge website (mathschallenge.net) is a bit more challenging. The craziness of manipulating radicals strikes again. This 2006 four-star problem from Colin Hughes at Maths Challenge is really astonishing, though it takes the right key to unlock it.
The craziness of manipulating radicals strikes again. This 2006 four-star problem from Colin Hughes at Maths Challenge is really astonishing, though it takes the right key to unlock it.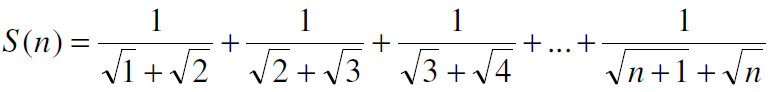
 This 2005 four-star problem from Colin Hughes at Maths Challenge is also a bit challenging.
This 2005 four-star problem from Colin Hughes at Maths Challenge is also a bit challenging.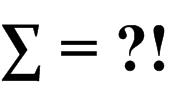 This is another stimulating math problem from Colin Hughes’s Maths Challenge website (mathschallenge.net).
This is another stimulating math problem from Colin Hughes’s Maths Challenge website (mathschallenge.net).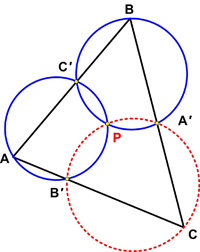 Here is yet another surprising result from Colin Hughes at Maths Challenge.
Here is yet another surprising result from Colin Hughes at Maths Challenge. This 2007 four-star problem from Colin Hughes at Maths Challenge is definitely a bit challenging.
This 2007 four-star problem from Colin Hughes at Maths Challenge is definitely a bit challenging.