This is a most surprising and amazing identity from the 1965 Polish Mathematical Olympiads.
“31. Prove that if n is a natural number, then we have
(√2 – 1)n = √m – √(m – 1),
where m is a natural number.”
Here, natural numbers are 1, 2, 3, …
I found it to be quite challenging, as all the Polish Math Olympiad problems seem to be.
See the Amazing Identity
Here is another challenging problem from the Polish Mathematical Olympiads. Its generality will cause more thought than for a simpler, specific problem.
“A cyclist sets off from point O and rides with constant velocity v along a rectilinear highway. A messenger, who is at a distance a from point O and at a distance b from the highway, wants to deliver a letter to the cyclist. What is the minimum velocity with which the messenger should run in order to attain his objective?”
See the Tired Messenger Problem
(Update 1/29/2025) Dan Steinitz Solution
Dan Steinitz from Israel has sent an elegant solution that only involves vectors and geometry without calculus. I have edited slightly his email and added excerpts from his whiteboard solution, though without the Hebrew annotations, which unfortunately I cannot read. But that is the glory of the universal language of mathematics: it can be read and understood in any language.
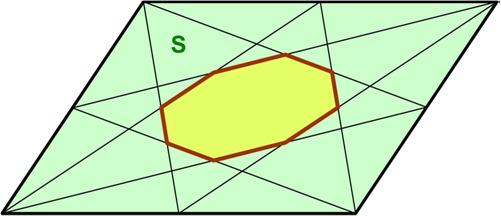Here is another problem from the Polish Mathematical Olympiads published in 1960.
“95. In a parallelogram of given area S each vertex has been connected with the mid-points of the opposite two sides. In this manner the parallelogram has been cut into parts, one of them being an octagon. Find the area of that octagon.”
See the Octagonal Area Problem for solutions.
Here is a slightly different kind of problem from the Polish Mathematical Olympiads.
“106. A beam of length a is suspended horizontally by its ends by means of two parallel ropes of lengths b. We twist the beam through an angle φ about the vertical axis passing through the centre of the beam. How far will the beam rise?”
See the Twisting Beam Problem for solutions.
Here is a challenging problem from the Polish Mathematical Olympiads published in 1960.
“22. Prove that the polynomial
x44 + x33 + x22 + x11 + 1
is divisible by the polynomial
x4 + x3 + x2 + x + 1.”
See the Polynomial Division Problem
(Update 8/23/2021) The idea expressed in this post that mathematicians are “lazy” and seek short-cuts to solving questions and problems, as I did in this one, was recently the subject of a Numberphile post by Marcus du Sautoy: “Mathematics is all about SHORTCUTS“.
