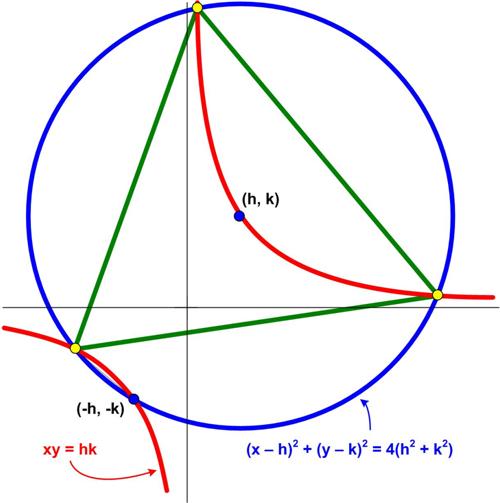
 Here is another simply amazing problem from Five Hundred Mathematical Challenges:
Here is another simply amazing problem from Five Hundred Mathematical Challenges:
“Problem 154. Show that three solutions, (x1,.y1), (x2,.y2), (x3, y3), of the four solutions of the simultaneous equations
____________(x – h)² + (y – k)² = 4(h² + k²)
______________________xy = hk
are vertices of an equilateral triangle. Give a geometrical interpretation.”
Again, I don’t see how anyone could have discovered this property involving a circle, a hyperbola, and an equilateral triangle. It seems plausible when h.=.k, but it is not at all obvious for h.≠.k. For some reason, I had difficulty getting a start on a solution, until the obvious approach dawned on me. I don’t know why it took me so long.
See the Amazing Triangle Problem.

 Here is another train puzzle, this time from J. A. H. Hunter’s Entertaining Mathematical Teasers:
Here is another train puzzle, this time from J. A. H. Hunter’s Entertaining Mathematical Teasers: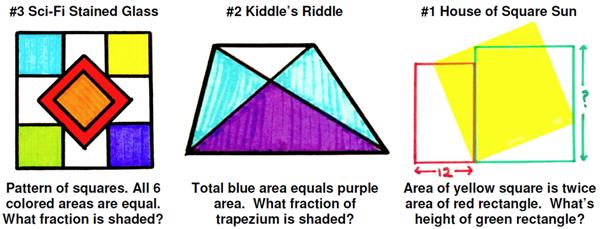 I have been subverted again by a recent post by Ben Orlin, “
I have been subverted again by a recent post by Ben Orlin, “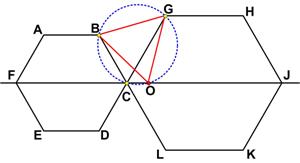 This is truly an amazing result from Five Hundred Mathematical Challenges.
This is truly an amazing result from Five Hundred Mathematical Challenges.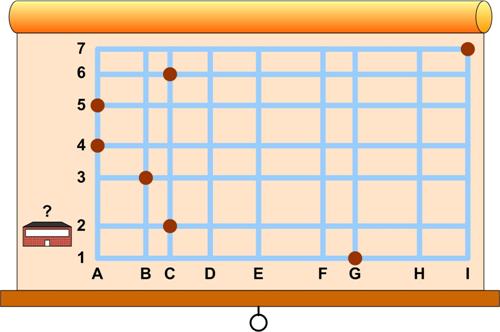 This is a somewhat elegant problem from the 1987 Discover magazine’s Brain Bogglers by Michael Stueben:
This is a somewhat elegant problem from the 1987 Discover magazine’s Brain Bogglers by Michael Stueben: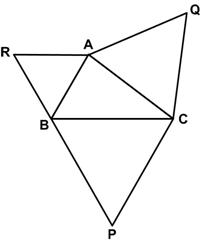 Here is another simple problem from Futility Closet.
Here is another simple problem from Futility Closet. Here is another Brain Bogglers problem from 1987.
Here is another Brain Bogglers problem from 1987.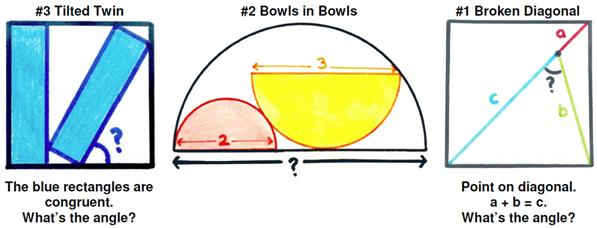
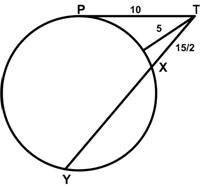 This is another problem from the Math Challenges section of the 2000 Pi in the Sky Canadian math magazine for high school students.
This is another problem from the Math Challenges section of the 2000 Pi in the Sky Canadian math magazine for high school students.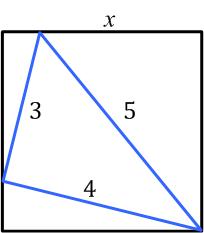 Presh Talwalkar had another interesting
Presh Talwalkar had another interesting