 This is another typical travel puzzle from the 2024 Math Calendar.
This is another typical travel puzzle from the 2024 Math Calendar.
“A boat travels downriver at 30 mph, then goes back up along the same path at 20 mph. What is the boat’s average speed?”
As before, recall that all the answers are integer days of the month.
See Another Boat Puzzle for a solution.

 This is a simple 1917 puzzle from Henry Dudeney.
This is a simple 1917 puzzle from Henry Dudeney. This is a problem from the 629 AD work of Bhaskara I, a contemporary of Brahmagupta.
This is a problem from the 629 AD work of Bhaskara I, a contemporary of Brahmagupta. This is a problem from the 2000 Olymon (the Mathematics Olympiads Correspondence Program) for secondary students sponsored jointly by the Canadian Mathematical Society and the Mathematics Department of the University of Toronto.
This is a problem from the 2000 Olymon (the Mathematics Olympiads Correspondence Program) for secondary students sponsored jointly by the Canadian Mathematical Society and the Mathematics Department of the University of Toronto.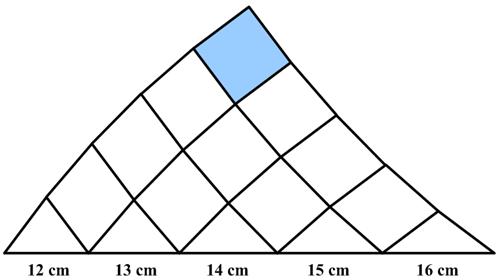 This is a
This is a 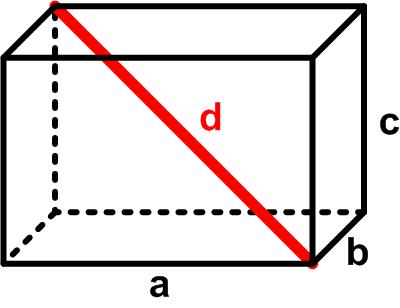 This is a slightly stimulating thought puzzle from Futility Closet.
This is a slightly stimulating thought puzzle from Futility Closet. This is a fairly straight-forward
This is a fairly straight-forward  This is a curious relation from the 2024 Math Calendar.
This is a curious relation from the 2024 Math Calendar.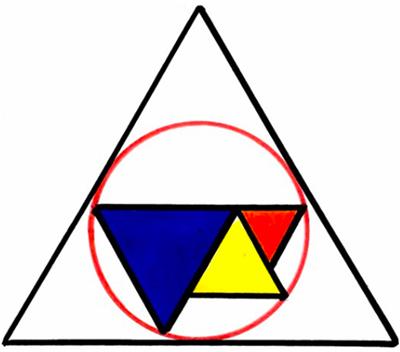 This is an old puzzle from Catriona Agg that I found on BL’s Math Games
This is an old puzzle from Catriona Agg that I found on BL’s Math Games  This is another problem from the c.100AD Chinese mathematical work, Jiǔ zhāng suàn shù (The Nine Chapters on the Mathematical Art) found at the MAA Convergence website Convergence.
This is another problem from the c.100AD Chinese mathematical work, Jiǔ zhāng suàn shù (The Nine Chapters on the Mathematical Art) found at the MAA Convergence website Convergence.