 Again we have a puzzle from the Sherlock Holmes puzzle book by Dr. Watson (aka Tim Dedopulos).
Again we have a puzzle from the Sherlock Holmes puzzle book by Dr. Watson (aka Tim Dedopulos).
“Our pursuit of the dubious Alan Grey, whom we encountered during The Adventure of the Third Carriage, led Holmes and myself to a circular running track where, as the sun fell, we witnessed a race using bicycles. There was some sort of substantial wager involved in the matter, as I recall, and the track had been closed off specially for the occasion. This was insufficient to prevent our ingress, obviously.
One of the competitors was wearing red, and the other blue. We never did discover their names. As the race started, red immediately pulled ahead. A few moments later, Holmes observed that if they maintained their pace, red would complete a lap in four minutes, whilst blue would complete one in seven.
Having made that pronouncement, he turned to me. ‘How long would it be before red passed blue if they kept those rates up, old chap?’
Whilst I wrestled with the answer, Holmes went back to watching the proceedings. Can you find the solution?”
Answer.
See the Track Problem for a solution.
 The craziness of manipulating radicals strikes again. This 2006 four-star problem from Colin Hughes at Maths Challenge is really astonishing, though it takes the right key to unlock it.
The craziness of manipulating radicals strikes again. This 2006 four-star problem from Colin Hughes at Maths Challenge is really astonishing, though it takes the right key to unlock it.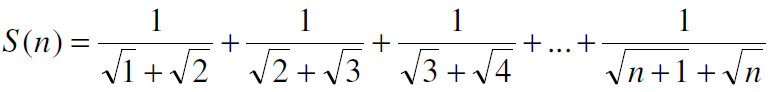

 Again we have a puzzle from the Sherlock Holmes puzzle book by Dr. Watson (aka Tim Dedopulos).
Again we have a puzzle from the Sherlock Holmes puzzle book by Dr. Watson (aka Tim Dedopulos). This is a cute little problem I came across via
This is a cute little problem I came across via  This is a nice variation on the typical clock problem posed by
This is a nice variation on the typical clock problem posed by 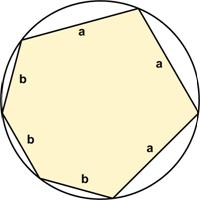 Here is another good problem from Five Hundred Mathematical Challenges:
Here is another good problem from Five Hundred Mathematical Challenges: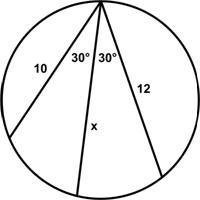 This is another challenging puzzle from
This is another challenging puzzle from 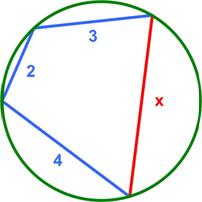
 Here is another Brainteaser from the Quantum magazine.
Here is another Brainteaser from the Quantum magazine. In looking through some old files I came across a math magazine I had bought in 1998. It was called Quantum and was published by the National Science Teachers Association in collaboration with the Russian magazine Kvant during the period 1990 to 2001 (coinciding with the Russian thaw, which in the following age of Putin seems eons ago). Fortunately, they are all online now. Besides some fascinating math articles the magazine contains a column of “Brainteasers.” Here is one of them:
In looking through some old files I came across a math magazine I had bought in 1998. It was called Quantum and was published by the National Science Teachers Association in collaboration with the Russian magazine Kvant during the period 1990 to 2001 (coinciding with the Russian thaw, which in the following age of Putin seems eons ago). Fortunately, they are all online now. Besides some fascinating math articles the magazine contains a column of “Brainteasers.” Here is one of them: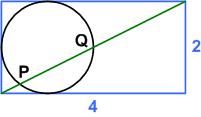 Here is another UKMT Senior Challenge problem from 2017, which has a straight-forward solution:
Here is another UKMT Senior Challenge problem from 2017, which has a straight-forward solution: