This is truly an amazing result from Five Hundred Mathematical Challenges.

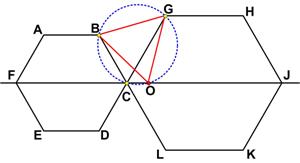
“Problem 119. Two unequal regular hexagons ABCDEF and CGHJKL touch each other at C and are so situated that F, C, and J are collinear.

Show that

(i) the circumcircle of BCG bisects FJ (at O say);
(ii) ΔBOG is equilateral.”

I wonder how anyone ever discovered this.

See the Magic Hexagons