Here is another Brainteaser from the Quantum magazine.
Here is another Brainteaser from the Quantum magazine.
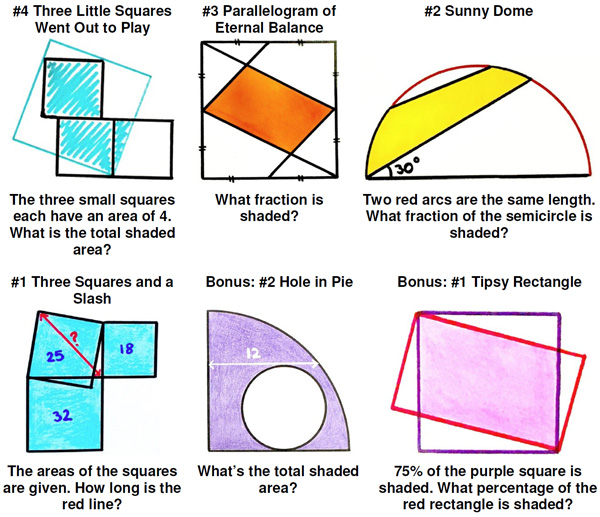
“Prove that the area of the red portion of the star is exactly half the area of the whole star. (N. Avilov)”
This is a relatively simple problem, but I wanted to include it because of its cartoon. Its implied gentle post-Soviet humor reminded me of that strange decade in US-Russian affairs between the end of the Cold War and the rise of Putin in the 21st century. The strangeness was brought home when we had our annual security checks of our classified document storage. Being mostly anti-submarine warfare (ASW) material the main concern was that it would not fall into the hands of the Soviets. But with the “demise” of the Soviet Union in 1989 no one cared any more about the classification. After decades of painfully securing these documents we could not suddenly turn them loose and throw them into the public trash. So we kept them secure anyway. You can imagine how we old cold-warriors feel about the current regime.
That is not to say that I didn’t welcome the thaw. Russian literature, both classical and even “Soviet realism”, as well as Russian cinema, is some of the world’s best. And Russian mathematicians have always been superior, and especially adept at communicating with novices. The collaboration of the American mathematicians and Kvant contributors in Quantum produced excellent results during the thaw. It is unfortunate that it could not survive the rise of Putin and his oligarchs.
See the Red Star
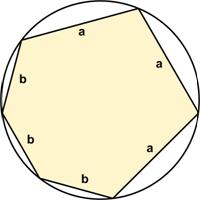 Here is another good problem from Five Hundred Mathematical Challenges:
Here is another good problem from Five Hundred Mathematical Challenges:
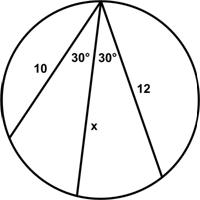 This is another challenging puzzle from
This is another challenging puzzle from 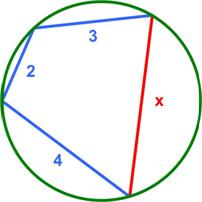
 Here is another Brainteaser from the Quantum magazine.
Here is another Brainteaser from the Quantum magazine. In looking through some old files I came across a math magazine I had bought in 1998. It was called Quantum and was published by the National Science Teachers Association in collaboration with the Russian magazine Kvant during the period 1990 to 2001 (coinciding with the Russian thaw, which in the following age of Putin seems eons ago). Fortunately, they are all online now. Besides some fascinating math articles the magazine contains a column of “Brainteasers.” Here is one of them:
In looking through some old files I came across a math magazine I had bought in 1998. It was called Quantum and was published by the National Science Teachers Association in collaboration with the Russian magazine Kvant during the period 1990 to 2001 (coinciding with the Russian thaw, which in the following age of Putin seems eons ago). Fortunately, they are all online now. Besides some fascinating math articles the magazine contains a column of “Brainteasers.” Here is one of them: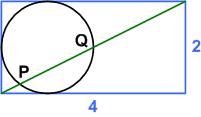 Here is another UKMT Senior Challenge problem from 2017, which has a straight-forward solution:
Here is another UKMT Senior Challenge problem from 2017, which has a straight-forward solution: A fun, relatively new, Sherlock Holmes puzzle book by Dr. Watson (aka Tim Dedopulos) has puzzles couched in terms of the Holmes-Watson banter. The following problem is a variation on the Sam Loyd
A fun, relatively new, Sherlock Holmes puzzle book by Dr. Watson (aka Tim Dedopulos) has puzzles couched in terms of the Holmes-Watson banter. The following problem is a variation on the Sam Loyd 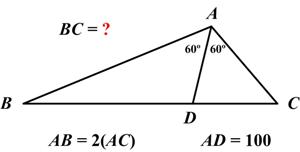 This is another problem from the indefatigable Presh Talwalkar.
This is another problem from the indefatigable Presh Talwalkar.