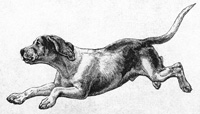
 Again we have a puzzle from the Sherlock Holmes puzzle book by Dr. Watson (aka Tim Dedopulos). This one is quite a bit more challenging, at least for me.
Again we have a puzzle from the Sherlock Holmes puzzle book by Dr. Watson (aka Tim Dedopulos). This one is quite a bit more challenging, at least for me.
“When Holmes and I met with Wiggins one afternoon, he was accompanied by a rather scrappy-looking mutt, who eyed me with evident suspicion.
‘This is Rufus,’ Wiggins said. ‘He’s a friend.’
‘Charmed,’ I said.
‘He’s very energetic,’ Wiggins told us. ‘Just this morning, he and I set out for a little walk.’
At the word ‘walk’, the dog barked happily.
‘When we set out, he immediately dashed off to the end of the road, then turned round and bounded back to me. He did this four times in total, in fact. After that, he settled down to match my speed, and we walked the remaining 81 feet to the end of the road at my pace. But it seems to me that if I tell you the distance from where we started to the end of the road, which is 625 feet, and that I was walking at four miles an hour, you ought to be able to work out how fast Rufus goes when he’s running.’
‘Indeed we should,’ said Holmes, and turned to look at me expectantly.
What’s the dog’s running speed?”
See the Rufus Puzzle for solutions.

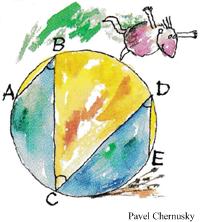 This is another delightful Brainteaser from the Quantum math magazine.
This is another delightful Brainteaser from the Quantum math magazine.
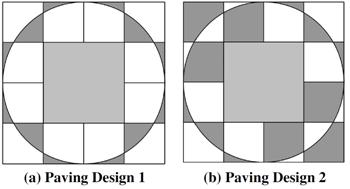 In my search for problems I decided to purchase Dan Griller’s GCSE problem book mentioned in the
In my search for problems I decided to purchase Dan Griller’s GCSE problem book mentioned in the  Here is a nice logic puzzle from 2014 Futility Closet.
Here is a nice logic puzzle from 2014 Futility Closet. For a change of pace, here is an early
For a change of pace, here is an early 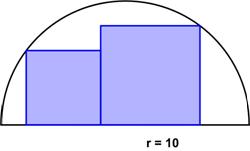 Yet another interesting problem from
Yet another interesting problem from  Here is a collection of puzzles from the great logic puzzle master Raymond Smullyan in a “Brain Bogglers” column for the 1996 Discover magazine.
Here is a collection of puzzles from the great logic puzzle master Raymond Smullyan in a “Brain Bogglers” column for the 1996 Discover magazine. This is a problem from the UKMT Senior Challenge for 2019. (It has been slightly edited to reflect the colors I added to the diagram.)
This is a problem from the UKMT Senior Challenge for 2019. (It has been slightly edited to reflect the colors I added to the diagram.) This is a nice Brainteaser from the Quantum math magazine.
This is a nice Brainteaser from the Quantum math magazine.