 Again we have a puzzle from the Sherlock Holmes puzzle book by Dr. Watson (aka Tim Dedopulos).
Again we have a puzzle from the Sherlock Holmes puzzle book by Dr. Watson (aka Tim Dedopulos).
“On one occasion, Holmes and I were asked to, solve the robbery of a number of dresses from the workshop of a recently deceased ladies’ tailor to the upper echelons of society. Holmes took a short look at the particulars of the case, and sent them all back to the gown-maker’s son with a scribbled note to the effect that it could only be one particular seamstress, with the help of her husband.
However, glancing through my observations some period later, I observed certain facts about the robbery which led me to an interesting little exercise. The stock at the workshop had been very recently valued at the princely sum of £1,800, and when examined after the theft, comprised of precisely 100 completed dresses in a range of styles, but of equal valuation. However, there was no remaining record of how many dresses had been there beforehand. The son did recall his father stating, of the valuation, that if he’d had thirty. dresses more, then a valuation of £1,800 would have meant £3 less per dress.
Are you able to calculate how many dresses were stolen?”
See the Fashion Puzzle for solutions.

 Ian Stewart has a nice logic problem in his Casebook of Mathematical Mysteries, which includes a pastiche of Sherlock Holmes in the form of Herlock Soames and Dr. Watsup, along with brother Spycraft and nemesis Dr. Mogiarty.
Ian Stewart has a nice logic problem in his Casebook of Mathematical Mysteries, which includes a pastiche of Sherlock Holmes in the form of Herlock Soames and Dr. Watsup, along with brother Spycraft and nemesis Dr. Mogiarty. This is another simple problem from H. E. Dudeney.
This is another simple problem from H. E. Dudeney.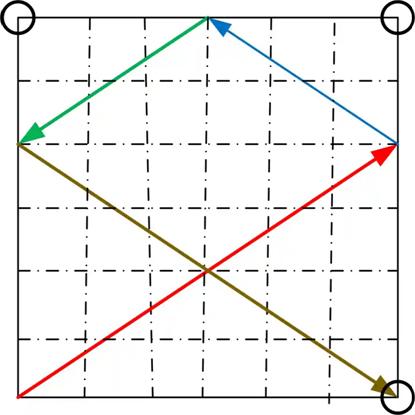 This is a nice
This is a nice 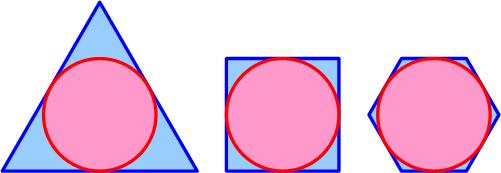 This surprising, but simple, puzzle is from the 12 April MathsMonday
This surprising, but simple, puzzle is from the 12 April MathsMonday 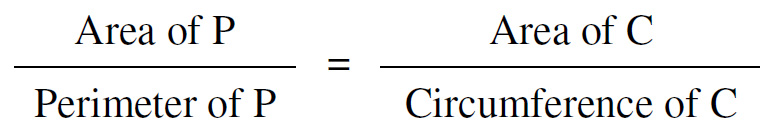
 This is a fairly straight-forward Brainteaser from the Quantum magazine.
This is a fairly straight-forward Brainteaser from the Quantum magazine. I braved another attempt at a Sam Loyd puzzle.
I braved another attempt at a Sam Loyd puzzle.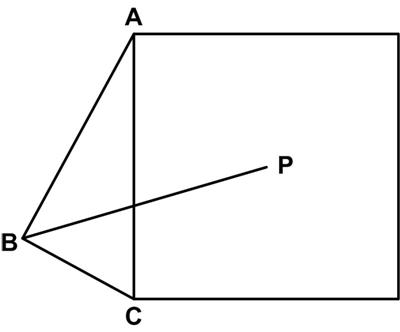 This is a simple problem from Five Hundred Mathematical Challenges:
This is a simple problem from Five Hundred Mathematical Challenges: Here is another, more challenging, problem from the Sherlock Holmes puzzle book by Dr. Watson (aka Tim Dedopulos).
Here is another, more challenging, problem from the Sherlock Holmes puzzle book by Dr. Watson (aka Tim Dedopulos). Here is a simple problem from an old
Here is a simple problem from an old