 Again we have a puzzle from the Sherlock Holmes puzzle book by Dr. Watson (aka Tim Dedopulos). This one is quite a bit more challenging, at least for me.
Again we have a puzzle from the Sherlock Holmes puzzle book by Dr. Watson (aka Tim Dedopulos). This one is quite a bit more challenging, at least for me.
“When Holmes and I met with Wiggins one afternoon, he was accompanied by a rather scrappy-looking mutt, who eyed me with evident suspicion.
‘This is Rufus,’ Wiggins said. ‘He’s a friend.’
‘Charmed,’ I said.
‘He’s very energetic,’ Wiggins told us. ‘Just this morning, he and I set out for a little walk.’
At the word ‘walk’, the dog barked happily.
‘When we set out, he immediately dashed off to the end of the road, then turned round and bounded back to me. He did this four times in total, in fact. After that, he settled down to match my speed, and we walked the remaining 81 feet to the end of the road at my pace. But it seems to me that if I tell you the distance from where we started to the end of the road, which is 625 feet, and that I was walking at four miles an hour, you ought to be able to work out how fast Rufus goes when he’s running.’
‘Indeed we should,’ said Holmes, and turned to look at me expectantly.
What’s the dog’s running speed?”
Answer.
See the Rufus Puzzle for solutions.

 Here is yet another problem from
Here is yet another problem from  Here is another delightful problem from the Sherlock Holmes puzzle book by Dr. Watson (aka Tim Dedopulos).
Here is another delightful problem from the Sherlock Holmes puzzle book by Dr. Watson (aka Tim Dedopulos). This is a nifty little problem from the Quantum math magazine.
This is a nifty little problem from the Quantum math magazine. This is a fun logic puzzle from one of Ian Stewart’s many math collections. I discovered that the problem actually is basically one of Lewis Carroll’s examples from an 1896 book:
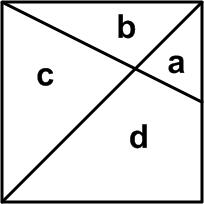
This is a fun logic puzzle from one of Ian Stewart’s many math collections. I discovered that the problem actually is basically one of Lewis Carroll’s examples from an 1896 book: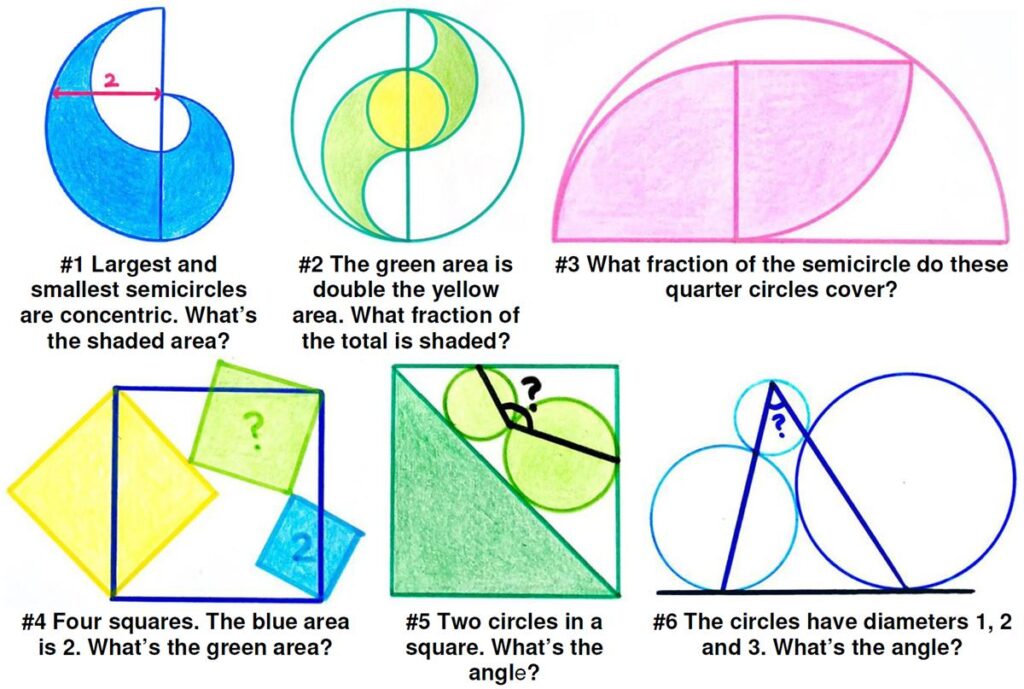
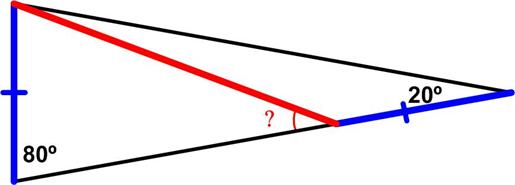
 Here is a simple Futility Closet problem from 2014.
Here is a simple Futility Closet problem from 2014. Here is a problem from Five Hundred Mathematical Challenges that I indeed found quite challenging.
Here is a problem from Five Hundred Mathematical Challenges that I indeed found quite challenging.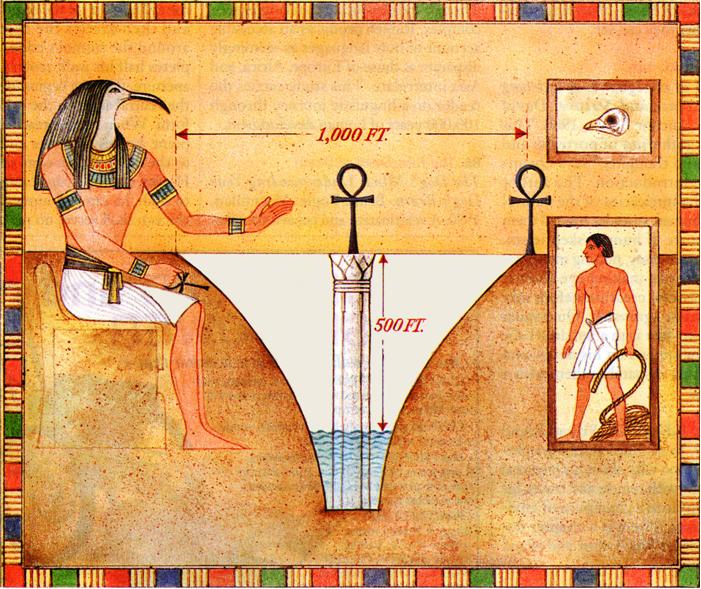 This is a nice puzzle from Clifford Pickover in the 1996 Discover magazine’s Brain Bogglers.
This is a nice puzzle from Clifford Pickover in the 1996 Discover magazine’s Brain Bogglers. Again we have a puzzle from the Sherlock Holmes puzzle book by Dr. Watson (aka Tim Dedopulos). This one is quite a bit more challenging, at least for me.
Again we have a puzzle from the Sherlock Holmes puzzle book by Dr. Watson (aka Tim Dedopulos). This one is quite a bit more challenging, at least for me.