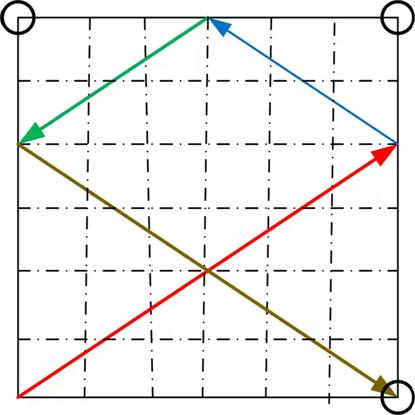
 This is a nice puzzle from Alex Bellos’s Monday Puzzle column in the Guardian.
This is a nice puzzle from Alex Bellos’s Monday Puzzle column in the Guardian.
“My cultural highlight of recent weeks has been the brilliant BBC documentary Gods of Snooker, about the time in the 1980s when the sport was a national obsession. Today’s puzzle describes a shot to malfunction the Romford Robot … and put the Whirlwind … in a spin.
Baize theorem
A square snooker table has three corner pockets, as [shown]. A ball is placed at the remaining corner (bottom left). Show that there is no way you can hit the ball so that it returns to its starting position.
The arrows represent one possible shot and how it would rebound around the table.
The table is a mathematical one, which means friction, damping, spin and napping do not exist. In other words, when the ball is hit, it moves in a straight line. The ball changes direction when it bounces off a cushion, with the outgoing angle equal to the incoming angle. The ball and the pockets are infinitely small (i.e. are points), and the ball does not lose momentum, so that its path can include any number of cushion bounces.
Thanks to Dr Pierre Chardaire, associate professor of computing science at the University of East Anglia, who devised today’s puzzle.”
See the Snooker Puzzle
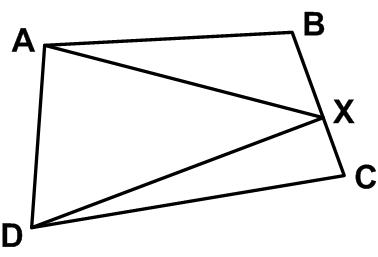 This is another simple problem from Five Hundred Mathematical Challenges:
This is another simple problem from Five Hundred Mathematical Challenges:
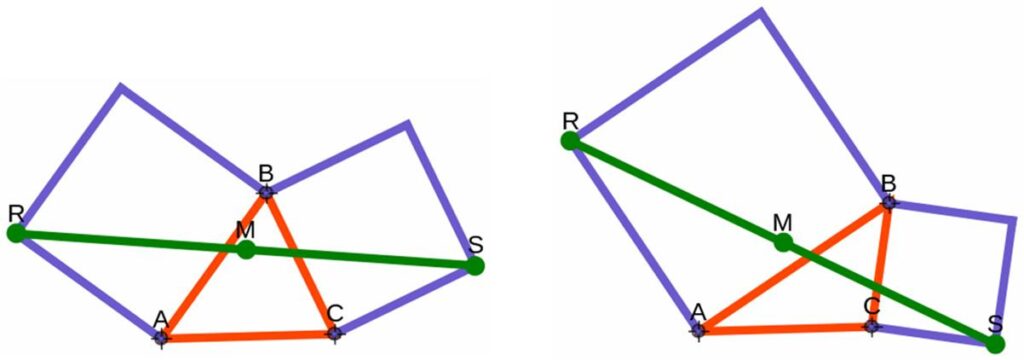
 This is a nice
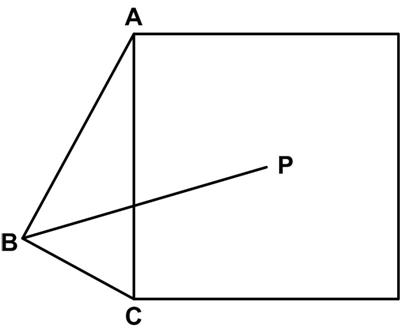
This is a nice  This surprising, but simple, puzzle is from the 12 April MathsMonday
This surprising, but simple, puzzle is from the 12 April MathsMonday 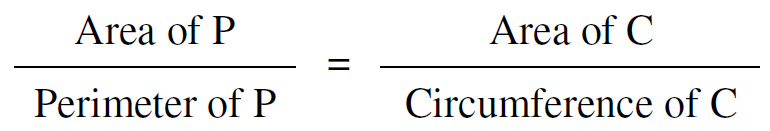
 This is a simple problem from Five Hundred Mathematical Challenges:
This is a simple problem from Five Hundred Mathematical Challenges: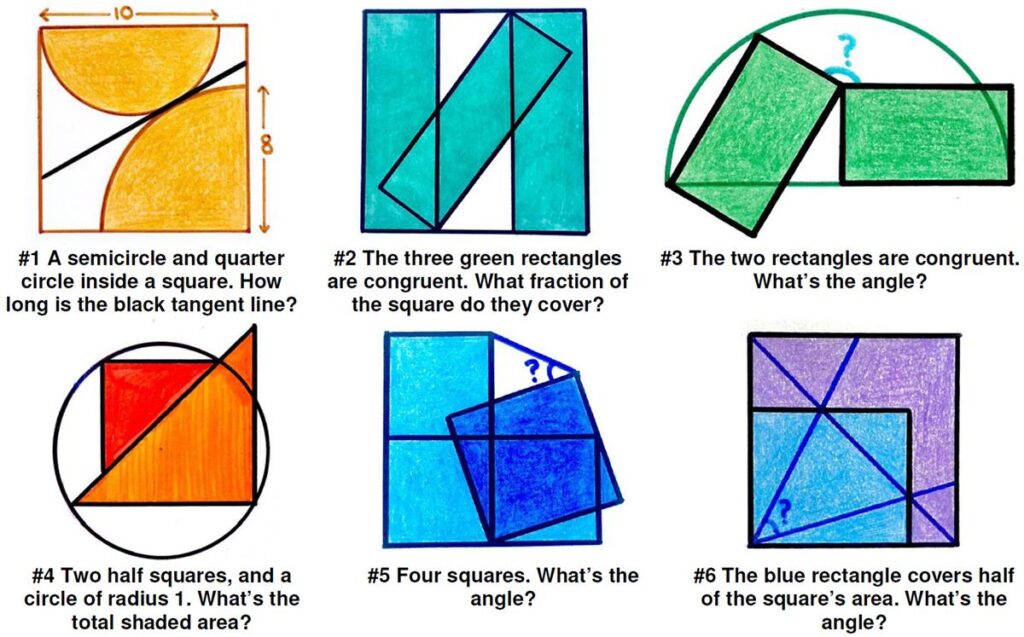 Here is yet another collection of beautiful geometric problems from Catriona Agg (née Shearer). For some reason I found these a bit more challenging than the previous ones. Some of them required more time to “see” the breakthrough.
Here is yet another collection of beautiful geometric problems from Catriona Agg (née Shearer). For some reason I found these a bit more challenging than the previous ones. Some of them required more time to “see” the breakthrough. This is another Brainteaser from the Quantum math magazine .
This is another Brainteaser from the Quantum math magazine .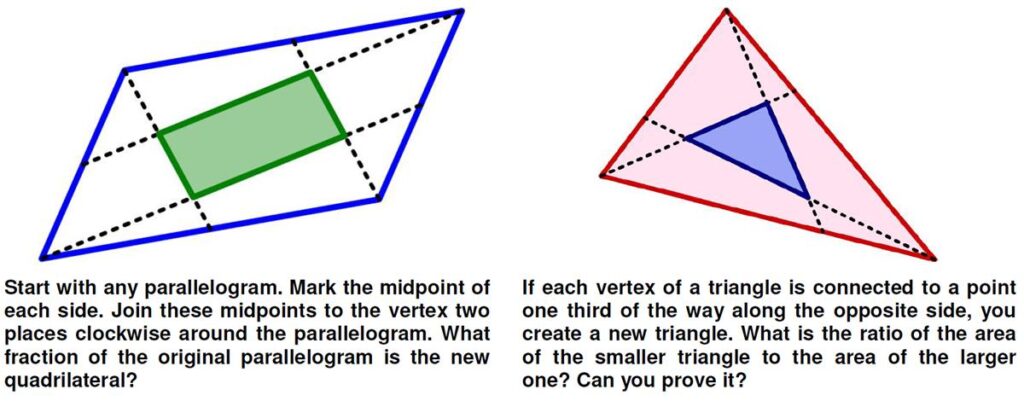 These two interesting problems were posed on MEI’s MathsMonday site on
These two interesting problems were posed on MEI’s MathsMonday site on 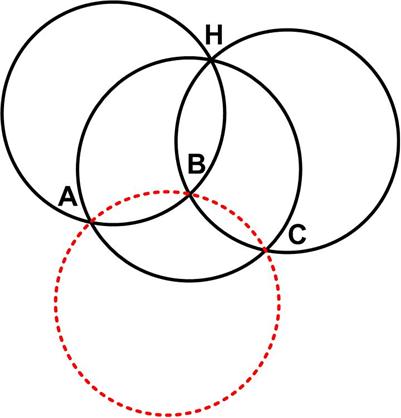 Here is a problem from the Quantum magazine, only this time from the “Challenges” section (these are expected to be a bit more difficult than the Brainteasers).
Here is a problem from the Quantum magazine, only this time from the “Challenges” section (these are expected to be a bit more difficult than the Brainteasers).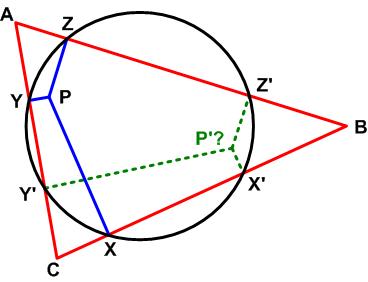 This is an interesting problem from the 1977 Canadian Math Society’s magazine, Crux Mathematicorum.
This is an interesting problem from the 1977 Canadian Math Society’s magazine, Crux Mathematicorum.