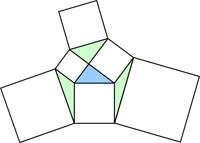
 This is a problem from the UKMT Senior Challenge for 2001. (It has been slightly edited to reflect the colors I added to the diagram.)
This is a problem from the UKMT Senior Challenge for 2001. (It has been slightly edited to reflect the colors I added to the diagram.)
“The [arbitrary] blue triangle is drawn, and a square is drawn on each of its edges. The three green triangles are then formed by drawing their lines which join vertices of the squares and a square is now drawn on each of these three lines. The total area of the original three squares is A1, and the total area of the three new squares is A2. Given that A2 = k A1, then
_____A_ k = 1_____B_ k = 3/2_____C_ k = 2_____D_ k = 3_____E_ more information is needed.”
I solved this problem using a Polya principle to simplify the situation, but UKMT’s solution was direct (and more complicated).
See the Six Squares Problem for solutions.

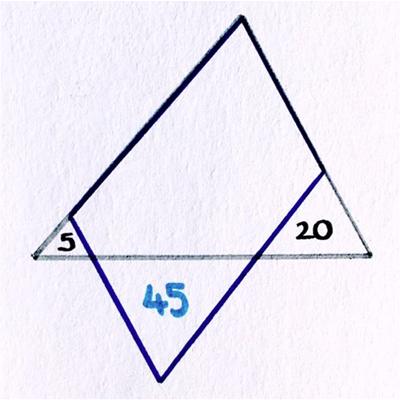
 Catriona Shearer retweeted the following problem from Antonio Rinaldi
Catriona Shearer retweeted the following problem from Antonio Rinaldi 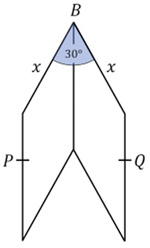 Another challenging problem from
Another challenging problem from 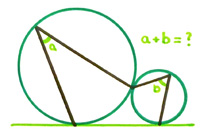 I really was trying to stop including
I really was trying to stop including 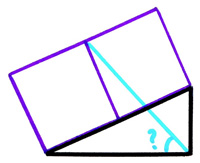 Since everyone by now who has any interest has gone directly to Catriona Shearer’s Twitter account for geometric puzzles, I was not going to include any more. But this one with its one-step solution is too fine to ignore and belongs with the “5 Problem” as one of the most elegant.
Since everyone by now who has any interest has gone directly to Catriona Shearer’s Twitter account for geometric puzzles, I was not going to include any more. But this one with its one-step solution is too fine to ignore and belongs with the “5 Problem” as one of the most elegant.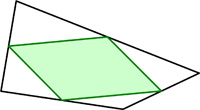 I came across this problem in Alfred Posamentier’s book, but I remember I had seen it a couple of places before and had never thought to solve it. At first, it seems like magic.
I came across this problem in Alfred Posamentier’s book, but I remember I had seen it a couple of places before and had never thought to solve it. At first, it seems like magic.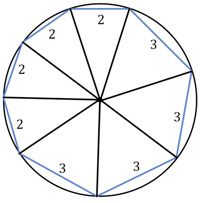 Here is a problem from the famous (infamous?) Putnam exam, presented by Presh Talwalkar. Needless to say, I did not solve it in 30 minutes—but at least I solved it (after making a blizzard of arithmetic and trigonometric errors).
Here is a problem from the famous (infamous?) Putnam exam, presented by Presh Talwalkar. Needless to say, I did not solve it in 30 minutes—but at least I solved it (after making a blizzard of arithmetic and trigonometric errors).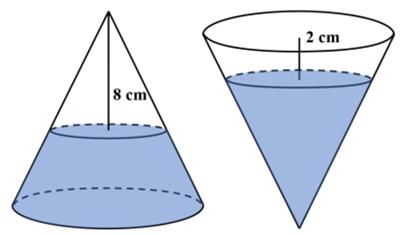 I was astonished that this problem was suitable for 8th graders. First of all the formula for the volume of a cone is one of the least-remembered of formulas, and I certainly never remember it. So my only viable approach was calculus, which is probably not a suitable solution for an 8th grader.
I was astonished that this problem was suitable for 8th graders. First of all the formula for the volume of a cone is one of the least-remembered of formulas, and I certainly never remember it. So my only viable approach was calculus, which is probably not a suitable solution for an 8th grader.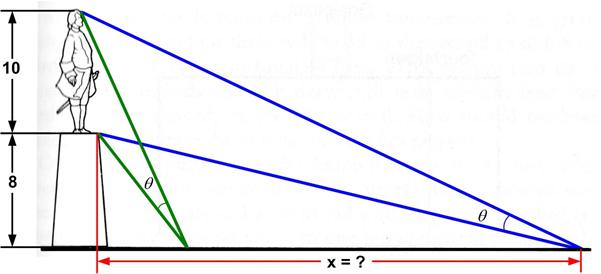 This is an old problem I had seen before. Here is David Wells’s rendition:
This is an old problem I had seen before. Here is David Wells’s rendition: