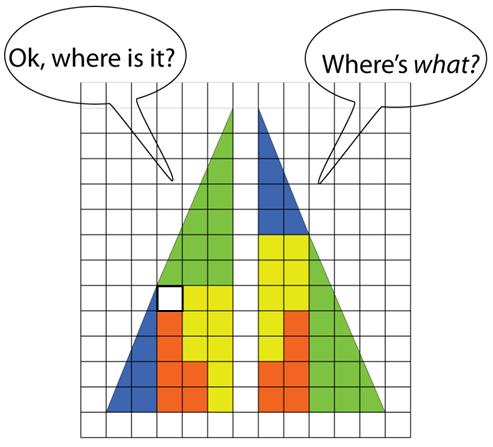
 Coming across this classic geometric paradox recently in Futility Closet motivated me to write down its solution in detail.
Coming across this classic geometric paradox recently in Futility Closet motivated me to write down its solution in detail.
“Where did the empty square come from?”
In any case, this is the canonical example for why I avoid visual geometric proofs—you can be so easily fooled. Real proofs require plane or analytic geometry arguments.
See the Classic Geometry Paradox
(Update 9/14/2024) Penn & Teller – Fool Us – Magic Trick
Continue reading

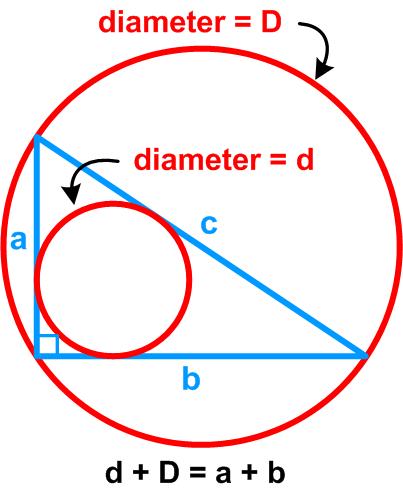
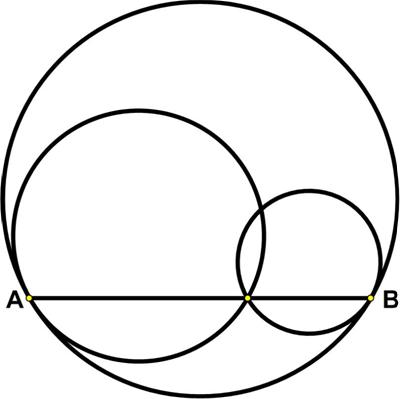 Here is another problem from the “Challenges” section of the Quantum magazine.
Here is another problem from the “Challenges” section of the Quantum magazine.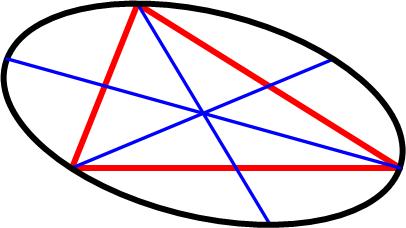 This is a tantalizing problem from the 1977 Crux Mathematicorum.
This is a tantalizing problem from the 1977 Crux Mathematicorum.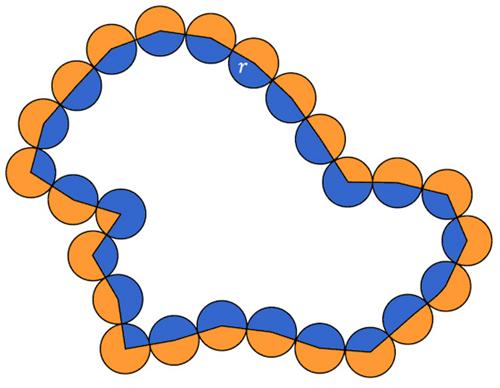 This is a nifty
This is a nifty  This is another puzzle from the Maths Masters team, Burkard Polster (aka Mathologer) and Marty Ross as part of their “Summer Quizzes” offerings.
This is another puzzle from the Maths Masters team, Burkard Polster (aka Mathologer) and Marty Ross as part of their “Summer Quizzes” offerings.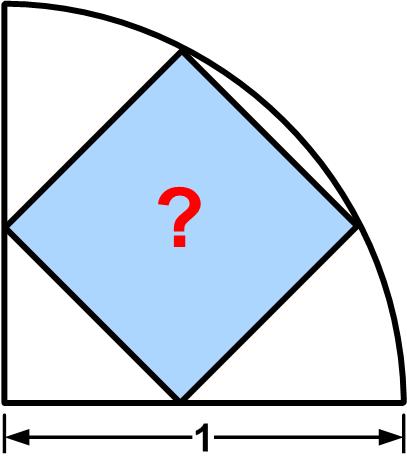 Another
Another 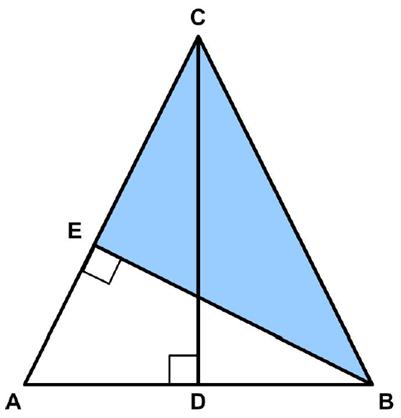 The Futility Closet website had the following
The Futility Closet website had the following 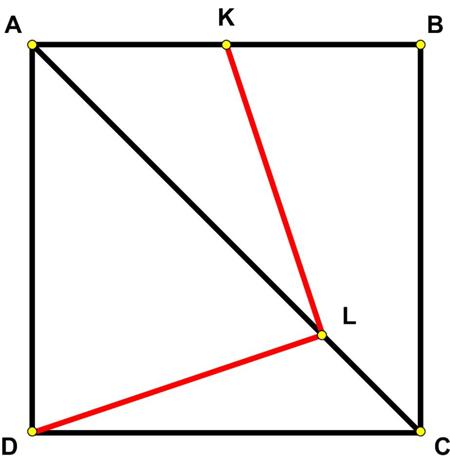 Here is another problem from the “Challenges” section of the Quantum magazine.
Here is another problem from the “Challenges” section of the Quantum magazine. This is a nice puzzle from the Maths Masters team, Burkard Polster (aka Mathologer) and Marty Ross as part of their “Summer Quizzes” offerings.
This is a nice puzzle from the Maths Masters team, Burkard Polster (aka Mathologer) and Marty Ross as part of their “Summer Quizzes” offerings.