 Here is a problem from the Quantum magazine, only this time from the “Challenges” section (these are expected to be a bit more difficult than the Brainteasers).
Here is a problem from the Quantum magazine, only this time from the “Challenges” section (these are expected to be a bit more difficult than the Brainteasers).
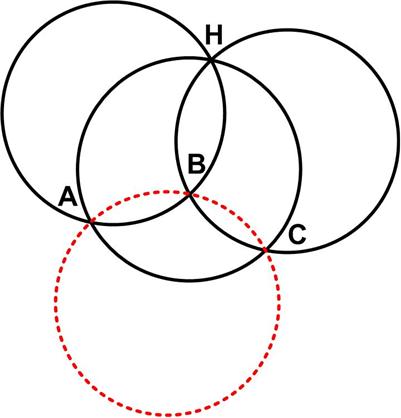
“Three circles with the same radius r all pass through a point H. Prove that the circle passing through the points where the pairs of circles intersect (that is, points A, B, and C) also has the same radius r.”
Indeed, I found this quite challenging. It took me several weeks to work out my approach and details.

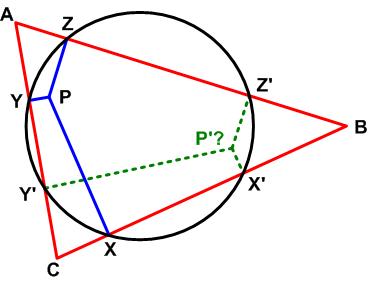 This is an interesting problem from the 1977 Canadian Math Society’s magazine, Crux Mathematicorum.
This is an interesting problem from the 1977 Canadian Math Society’s magazine, Crux Mathematicorum.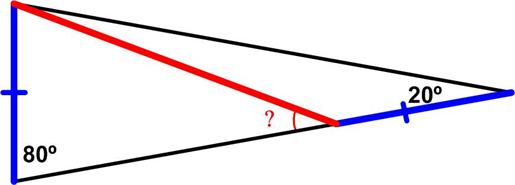 Here is yet another problem from
Here is yet another problem from 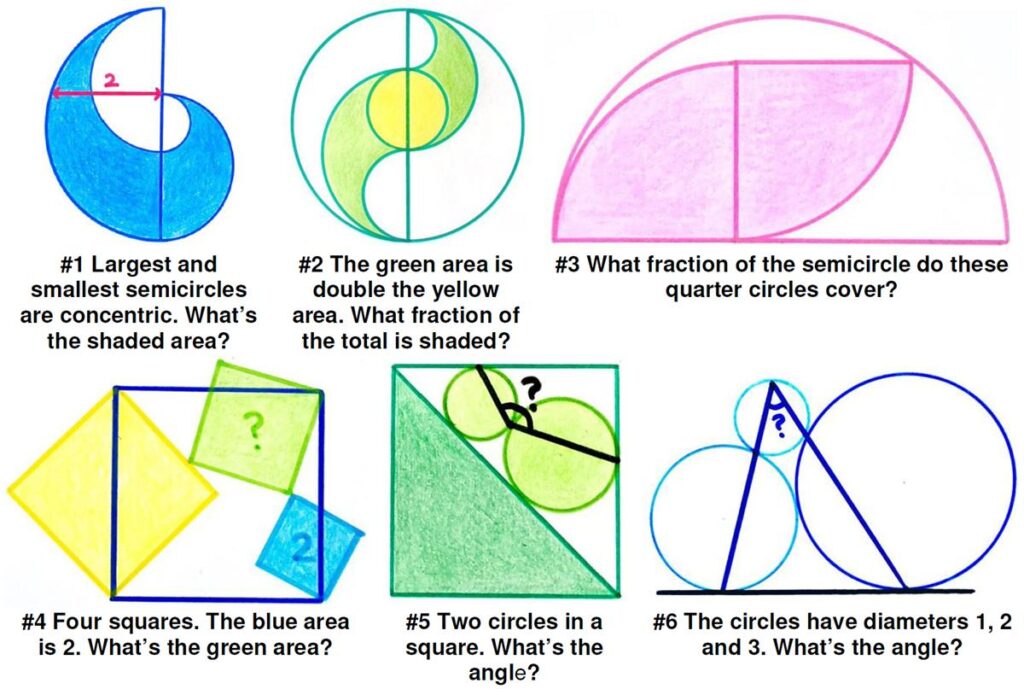
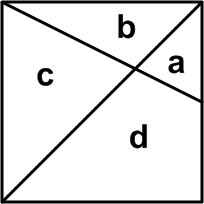 Here is a simple Futility Closet problem from 2014.
Here is a simple Futility Closet problem from 2014.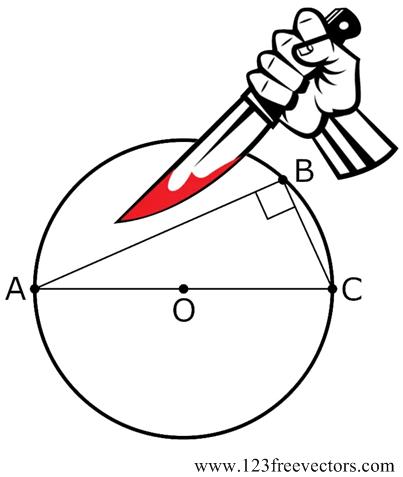 One of my favorite bloggers, Kevin Drum, decided to relieve the tedium of our current political anarchy by whacking the hornets’ nest of the high school mathematics curriculum, in particular the subject of plane geometry. You can tell from the tag list on my blog that I hold plane geometry in high regard and can’t let this gibe pass without some rebuttal, futile as it may be. Actually, I am not going to weigh in on the general issue of the current math curriculum that much, but rather make a few observations from my own experience over the years as it relates to
One of my favorite bloggers, Kevin Drum, decided to relieve the tedium of our current political anarchy by whacking the hornets’ nest of the high school mathematics curriculum, in particular the subject of plane geometry. You can tell from the tag list on my blog that I hold plane geometry in high regard and can’t let this gibe pass without some rebuttal, futile as it may be. Actually, I am not going to weigh in on the general issue of the current math curriculum that much, but rather make a few observations from my own experience over the years as it relates to  Here is a problem from Five Hundred Mathematical Challenges that I indeed found quite challenging.
Here is a problem from Five Hundred Mathematical Challenges that I indeed found quite challenging.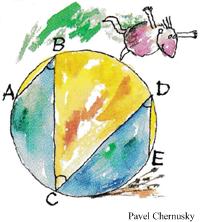 This is another delightful Brainteaser from the Quantum math magazine.
This is another delightful Brainteaser from the Quantum math magazine.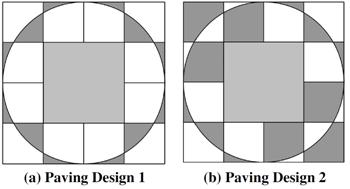 In my search for problems I decided to purchase Dan Griller’s GCSE problem book mentioned in the
In my search for problems I decided to purchase Dan Griller’s GCSE problem book mentioned in the  This is a problem from the UKMT Senior Challenge for 2019. (It has been slightly edited to reflect the colors I added to the diagram.)
This is a problem from the UKMT Senior Challenge for 2019. (It has been slightly edited to reflect the colors I added to the diagram.)