 Via Alex Bellos I found another Russian math magazine with fun problems. It is called Kvantik and Tanya Khovanova has a description (2015):
Via Alex Bellos I found another Russian math magazine with fun problems. It is called Kvantik and Tanya Khovanova has a description (2015):
“Kvant [Quantum] was a very popular science magazine in Soviet Russia. It was targeted to high-school children and I was a subscriber. Recently I discovered that a new magazine appeared in Russia. It is called Kvantik, which means Little Kvant. It is a science magazine for middle-school children. The previous years’ archives are available online in Russian. I looked at 2012, the first publication year, and loved it.”
Unfortunately, the magazine is in Russian and the later issues are only partially given online. To get the full magazine you need to subscribe. I used Google Translate and the mathematical context to render the English. Here is an interesting geometric problem that I would have thought to be quite challenging for middle schoolers.
“The vertices of the two squares are joined by two segments, as in the figure. It is given that these segments are equal. Find the angle between them.
Egor Bakaev”
See the Two Squares Problem for a solution.
(Update 8/22/2022, 9/1/2022) Simpler Solution, Simplest Solution!
Continue reading

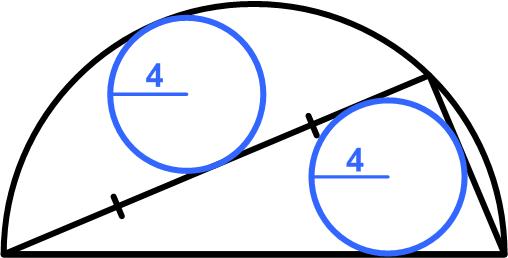 Here is a problem from the 2022 Math Calendar.
Here is a problem from the 2022 Math Calendar. I have just finished reading a most remarkable book by Alec Wilkinson, called A Divine Language: Learning Algebra, Geometry, and Calculus at the Edge of Old Age. I had read an
I have just finished reading a most remarkable book by Alec Wilkinson, called A Divine Language: Learning Algebra, Geometry, and Calculus at the Edge of Old Age. I had read an 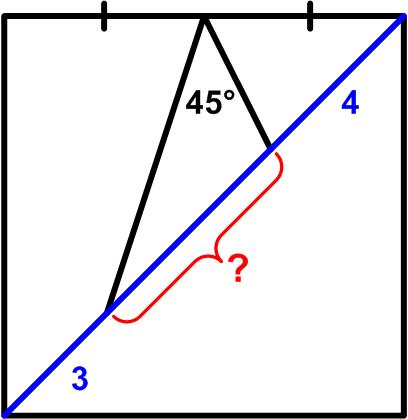 Henk Reuling posted a deceptively simple-looking geometric
Henk Reuling posted a deceptively simple-looking geometric 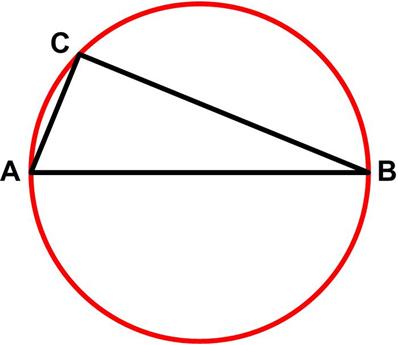 This math problem from Colin Hughes’s Maths Challenge website (mathschallenge.net) is a bit more challenging.
This math problem from Colin Hughes’s Maths Challenge website (mathschallenge.net) is a bit more challenging.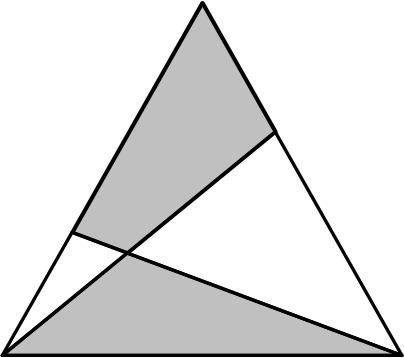 This is another fairly simple puzzle from Futility Closet from a while ago (2014).
This is another fairly simple puzzle from Futility Closet from a while ago (2014).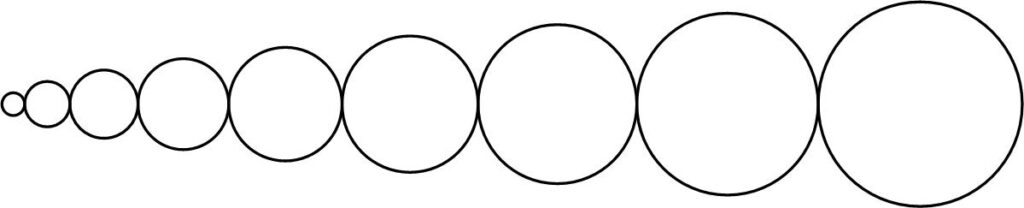
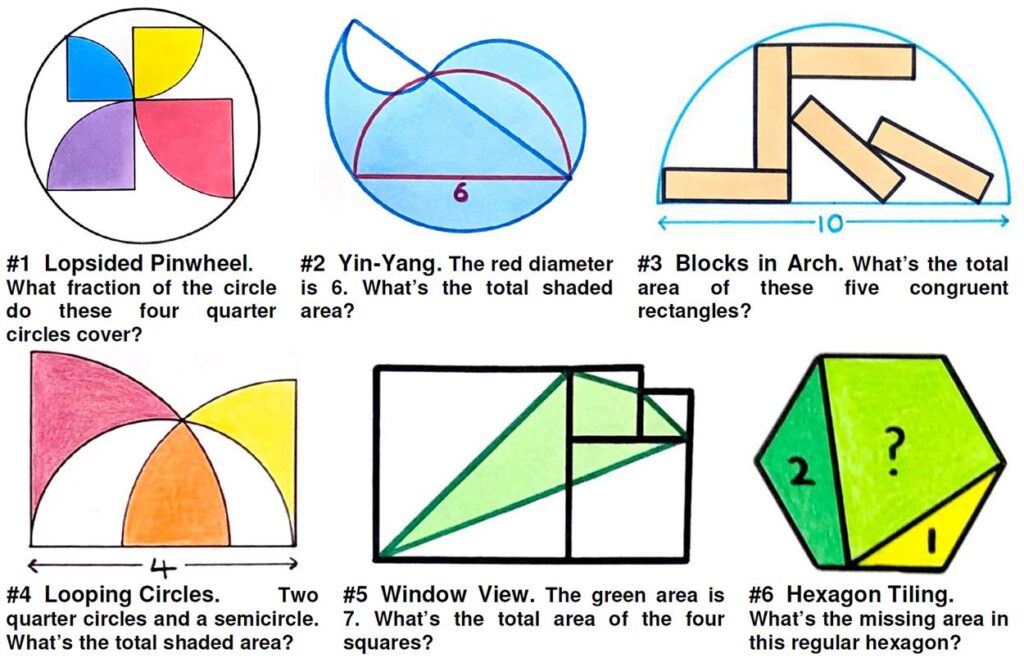 Here is yet another (belated) collection of beautiful geometric problems from Catriona Agg (née Shearer).
Here is yet another (belated) collection of beautiful geometric problems from Catriona Agg (née Shearer).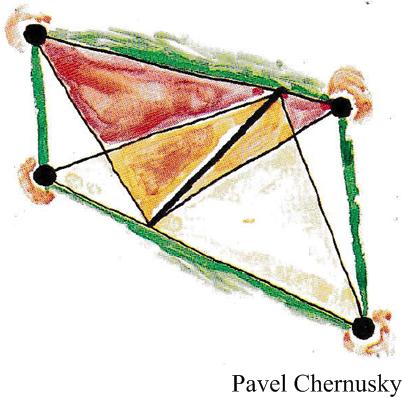 Here is another elegant Quantum math magazine Brainteaser from the imaginative V. Proizvolov.
Here is another elegant Quantum math magazine Brainteaser from the imaginative V. Proizvolov.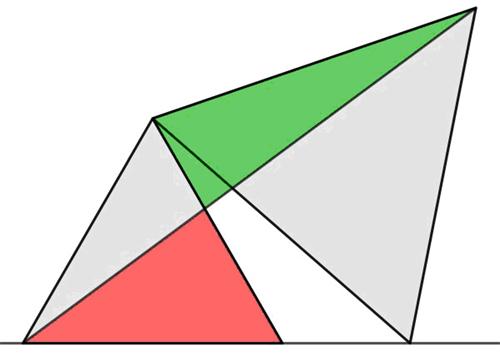 This is a most interesting problem proposed by
This is a most interesting problem proposed by