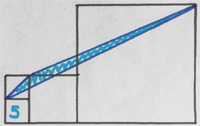
 This is a collection of simple but elegant puzzles, mostly from a British high school math teacher Catriona Shearer, for which I thought I would show solutions (solutions for a number of them had not been posted yet on Twitter at the time of writing). See the Geometric Puzzle Medley.
This is a collection of simple but elegant puzzles, mostly from a British high school math teacher Catriona Shearer, for which I thought I would show solutions (solutions for a number of them had not been posted yet on Twitter at the time of writing). See the Geometric Puzzle Medley.
Apparently Catriona Shearer creates these problems herself, which shows an especially gifted talent. Ben Olin, of Math with Bad Drawings fame, had an interesting interview with Ms. Shearer. The reason for the interest in her work becomes evident the more of her geometry problems one sees. They are especially elegant and minimalist, and often have simple solutions, as exemplified by the “5 Problem” or “Shear Beauty” problem illustrated here. Words, such as “beauty” and “elegance”, are often bandied about concerning various mathematical subjects, but as with any discussion of esthetics, the efforts at explanation usually fall flat. Shearer’s problems are one of the best examples of these ideas I have ever seen. If you contemplate her problems and even solve them, you will understand the meaning of these descriptions.
One of the key aspects of mathematics is often its “hidden-ness” (some would say “opacity” or “incomprehension”). Her problems appear to have insufficient information to solve. But as you look at the usually regular figures, you see that there are inherent rigid constraints that soon yield specific information that leads to a solution. This discovery is akin to the sensation of discovering Newton’s mathematical laws underlying physical reality. It is the essence of one of the joys of mathematics.
Continue reading →
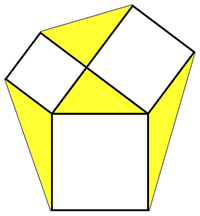 From Futility Closet we have another intriguing problem with what turns out to be a simple and elegant solution.
From Futility Closet we have another intriguing problem with what turns out to be a simple and elegant solution.
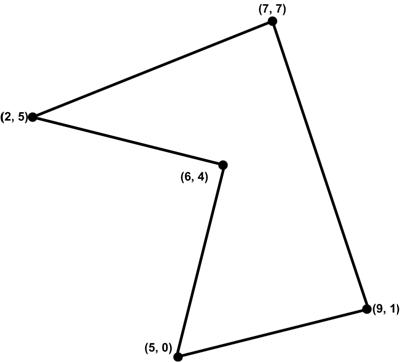 This is another problem from
This is another problem from 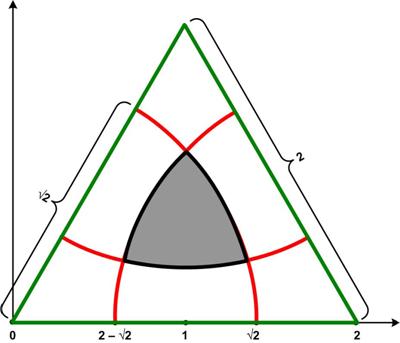 This article is basically a technical footnote without wider significance. At the time I had been reading with interest Paul J. Nahin’s latest book Number-Crunching (2011). Nahin presents a problem that he will solve with the Monte Carlo sampling approach.
This article is basically a technical footnote without wider significance. At the time I had been reading with interest Paul J. Nahin’s latest book Number-Crunching (2011). Nahin presents a problem that he will solve with the Monte Carlo sampling approach.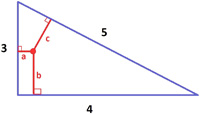 James Tanton
James Tanton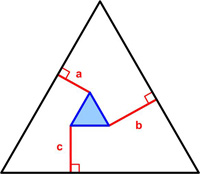 I found this collection of related problems by
I found this collection of related problems by  This is a collection of simple but elegant puzzles, mostly from a British high school math teacher
This is a collection of simple but elegant puzzles, mostly from a British high school math teacher 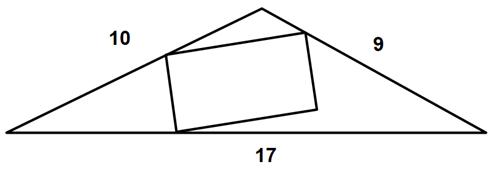 This problem comes from the defunct Wall Street Journal Varsity Math Week collection.
This problem comes from the defunct Wall Street Journal Varsity Math Week collection.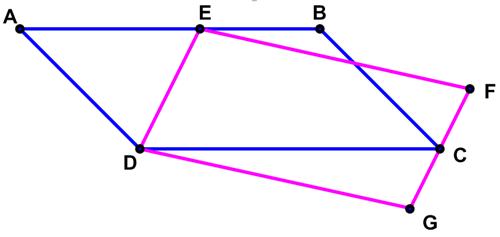 Yet another
Yet another 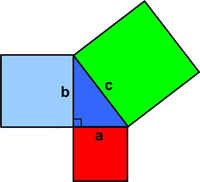 All too frequently I come across the usual statements questioning why non-technical folks should bother studying math. A typical example is the Pythagorean Theorem. People say, “What good is that? I’ll never use it. So why bother?” Ah, the famous “utility” argument – as if everything worthwhile must be “useful.” I thought I would take this “useless” math example par excellence and show that, in fact, it harbors many of the best aspects of mathematics that anyone should find appealing. See the
All too frequently I come across the usual statements questioning why non-technical folks should bother studying math. A typical example is the Pythagorean Theorem. People say, “What good is that? I’ll never use it. So why bother?” Ah, the famous “utility” argument – as if everything worthwhile must be “useful.” I thought I would take this “useless” math example par excellence and show that, in fact, it harbors many of the best aspects of mathematics that anyone should find appealing. See the 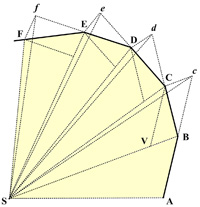 I have long been fascinated by Newton’s proof of Kepler’s Equal Areas Law and wanted to write about it. Of course, others have as well, but I wanted to emphasize an aspect of the proof that supported my philosophy of mathematics.
I have long been fascinated by Newton’s proof of Kepler’s Equal Areas Law and wanted to write about it. Of course, others have as well, but I wanted to emphasize an aspect of the proof that supported my philosophy of mathematics.