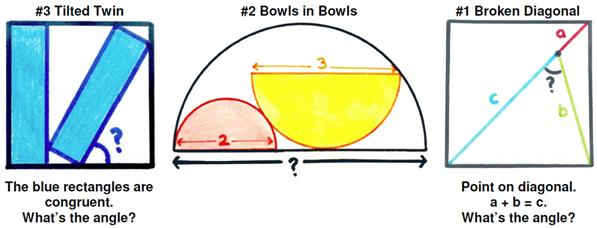
I was really trying to avoid getting pulled into more addictive geometric challenges from Catriona Shearer (since they can consume your every waking moment), but a recent post by Ben Orlin, “The Tilted Twin (and other delights),” undermined my intent. As Orlin put it, “This is a countdown of her three favorite puzzles from October 2019” and they are vintage Shearer. You should check out Olin’s website since there are “Mild hints in the text; full spoilers in the comments.” He also has some interesting links to other people’s efforts. (Olin did leave out a crucial part of #1, however, which caused me to think the problem under-determined. Checking Catriona Shearer’s Twitter I found the correct statement, which I have used here.)
I have to admit, I personally found the difficulty of these puzzles a bit more challenging than before (unless I am getting rusty) and the difficulty in the order Olin listed. Again, the solutions (I found) are simple but mostly tricky to discover. I solved the problems before looking at Olin’s or others’ solutions.
See the Geometric Puzzle Mayhem.

 This is another problem from the Math Challenges section of the 2000 Pi in the Sky Canadian math magazine for high school students.
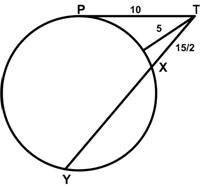
This is another problem from the Math Challenges section of the 2000 Pi in the Sky Canadian math magazine for high school students.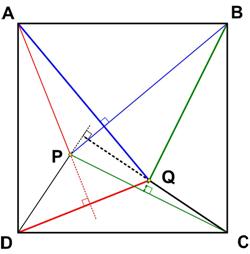 I found this problem from the Math Challenges section of the 2002 Pi in the Sky Canadian math magazine for high school students to be truly astonishing.
I found this problem from the Math Challenges section of the 2002 Pi in the Sky Canadian math magazine for high school students to be truly astonishing.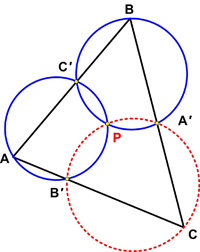 Here is yet another surprising result from Colin Hughes at Maths Challenge.
Here is yet another surprising result from Colin Hughes at Maths Challenge. This is from the UKMT Senior Challenge of 2004.
This is from the UKMT Senior Challenge of 2004.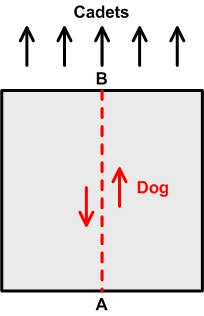 In my search for new problems I came across this one from Martin Gardner:
In my search for new problems I came across this one from Martin Gardner: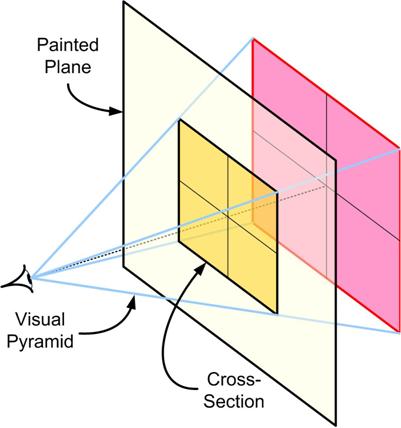 I was reading yet another book on the Scientific Revolution when I came across a discussion of the mathematical significance of the invention of perspective for painting in the 15th century Italian Renaissance. The main player in the saga was Leon Battista Alberti (1404 – 1472) and his tome De Pictura (On Painting) (1435-6), which contained the first mathematical presentation of perspective. Even though mathematics was advertised, it was not at the level of trigonometry I used in my post “
I was reading yet another book on the Scientific Revolution when I came across a discussion of the mathematical significance of the invention of perspective for painting in the 15th century Italian Renaissance. The main player in the saga was Leon Battista Alberti (1404 – 1472) and his tome De Pictura (On Painting) (1435-6), which contained the first mathematical presentation of perspective. Even though mathematics was advertised, it was not at the level of trigonometry I used in my post “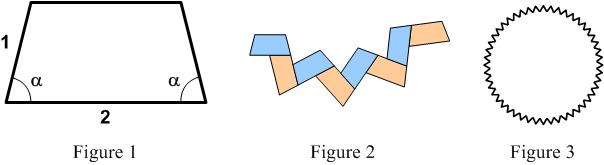 How many tiles are there in the complete pattern?
How many tiles are there in the complete pattern?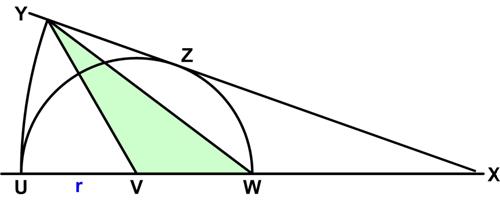 Here is a problem from the UKMT Senior (17-18 year-old) Mathematics Challenge for 2012:
Here is a problem from the UKMT Senior (17-18 year-old) Mathematics Challenge for 2012: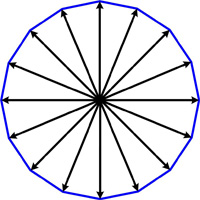 This is a fun problem from Mathematical Quickies (1967).
This is a fun problem from Mathematical Quickies (1967).